题目内容
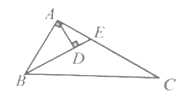
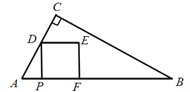
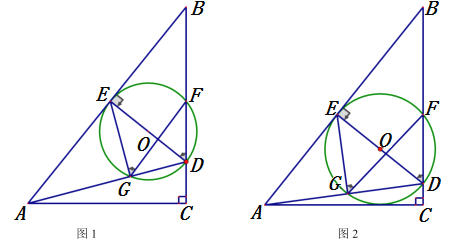
【题目】如图1,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为斜边
为斜边![]() 上一个动点,作
上一个动点,作![]() ,交直角边
,交直角边![]() 于点
于点![]() ,以
,以![]() 为直径作
为直径作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 交
交![]() 于点
于点![]() .连结
.连结![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)求证:![]() ;
;
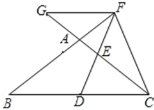
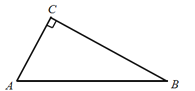
(3)如图2,当![]() 与边
与边![]() 相切时,求
相切时,求![]() 的直径;
的直径;
(4)若以![]() 为顶点的三角形是等腰三角形时,求所有满足条件的
为顶点的三角形是等腰三角形时,求所有满足条件的![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ;(4)
;(4)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用![]() ,即可得出结论;
,即可得出结论;
(2)利用同弧所对的圆周角相等得出![]() ,利用同角的余角相等得出
,利用同角的余角相等得出![]() ,从而得出结论;
,从而得出结论;
(3)作![]() ,
,![]() ,则
,则![]() ,
,![]() ,利用
,利用![]() 得出
得出![]() ,进而得出直径;
,进而得出直径;
(4)分![]() 、
、![]() 、
、![]() 三种情况讨论即可.
三种情况讨论即可.
(1)解:在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中
中
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]()
解得:![]() ,
,
∴![]() ,
,![]() ,
,
(2)证明:∵![]()
∴![]() .
.
又∵![]() .
.
∴![]() .
.
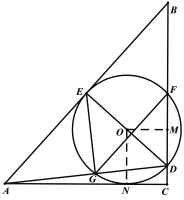
解:(3)作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,
∵![]() 与
与![]() 相切,∴
相切,∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]()
∴![]() ∴
∴![]()
∴![]() 的直径为
的直径为![]() ;
;
(4)若以![]() 为顶点的三角形是等腰三角形,则可分为三种情况:
为顶点的三角形是等腰三角形,则可分为三种情况:
①当![]() 时,
时,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,即
,即![]()
∵![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中,
中,
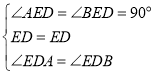 ,
,
∴![]()
∴![]() ,
,
∴![]()
∴![]() ;
;
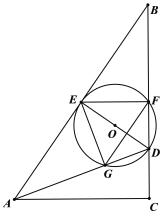
②当![]() 时,
时,
∵![]() 为直径,∴
为直径,∴![]() ,即
,即![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵四边形![]() 内接于
内接于![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即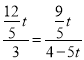 ,
,
解得:![]() ,
,
经检验:![]() 是原方程的解,
是原方程的解,
∴![]() ;
;
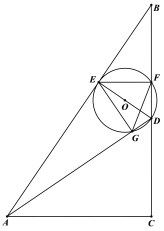
③当![]() 时,
时,
∵![]() ,∴
,∴![]() ,
,
∵四边形![]() 内接于
内接于![]() ,
,
∴![]() ,
,![]() ,即
,即![]()
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵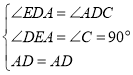 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
综上所述:当![]() 或
或![]() 或
或![]() 时,以
时,以![]() 为顶点的三角形是等腰三角形.
为顶点的三角形是等腰三角形.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目