题目内容
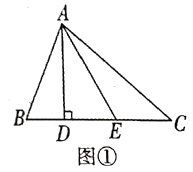
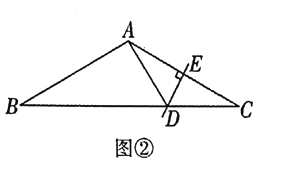
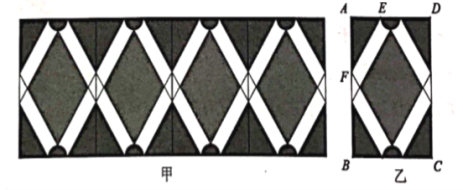
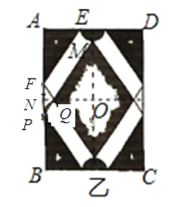
【题目】图甲是小明设计的花边图案作品该作品由形如图乙的矩形图案拼接而成(不重叠,无缝隙).该矩形图案既是轴对称图形,又是中心对称图形.图乙中,![]() ,上、下两个半圆的面积之和为
,上、下两个半圆的面积之和为![]() ,中间阴影菱形的一组对边与
,中间阴影菱形的一组对边与![]() 平行,且菱形的面积比
平行,且菱形的面积比![]() 个角上的阴影三角形的面积之和大
个角上的阴影三角形的面积之和大![]() ,则
,则![]() 的长度为__________
的长度为__________![]()
【答案】![]()
【解析】
由面积求圆的半径,设AE=2k,AF=3k,由平行将菱形的对角线用比例表示,设MO=3m,OQ=2m,根据已知条件推导出m-k=![]() ,m+k=6,进而求值;
,m+k=6,进而求值;
解:作菱形对角线交于点O,MO,QO分别是对角线的一半,
设左侧三角形与对角线的一个交点N,
∵, 设AE=2k,AF=3k, 由上下两个半圆面积和4π,
∴半径r=2,
∵中间阴影菱形的一组对边与EF平行,
∴ ![]() 设MO=3m,OQ=2m,
设MO=3m,OQ=2m,
在△NPQ中, ![]()
∴AB=6m+4, NQ=2k+2-2m,
∴NP=3k+3-3m,
∴AB=6k+6-6m+6k![]() ,
,
∴m-k=![]() ,
,
菱形的面积比4个角上的阴影三角形的面积之和大12cm2,
∴12k2+12=12m2,
∴(m+k)(m-k)=1,
∴m+k=6,
∴m=![]() ,
,
∴AB=![]() ;
;
故答案 ![]() ;
;

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
【题目】黄山毛峰是中国十大名茶之一 ,产于安徽省黄山(徽州)一带,也称徽茶.有诗日:“未见黄山面,十里闻茶香”.某茶庄以![]() 元
元![]() 的价格收购一批毛峰,物价部门规定销售单价不低于成本且不得超过成本的
的价格收购一批毛峰,物价部门规定销售单价不低于成本且不得超过成本的![]() 倍,经试销过发现,日销量
倍,经试销过发现,日销量![]() 与销售单价
与销售单价![]() 的对应关系如下表:且
的对应关系如下表:且![]() 与
与![]() 满足初中所学某种函数关系.
满足初中所学某种函数关系.
|
|
|
|
| ··· |
|
|
|
|
| ··· |
(1)根据表格,求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)在销售过程中,每日还需支付其他费用![]() 元,当销售单价为多少时,该茶庄日利润最大?最大利润是多少元?
元,当销售单价为多少时,该茶庄日利润最大?最大利润是多少元?