Question

【题目】如图，在平面直角坐标系中，直线与双曲线相交于A、B两点，C是第一象限内的双曲线上与点A不重合的一点，连接CA并延长交y轴于点P，连接BP，BC。若点A坐标 （2，3），△PBC的面积是24，则点C坐标为（ ）

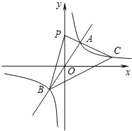
A. （3，1） B. （3，2） C. （6，2） D. （6，1）

Answer 1

【答案】D

【解析】分析：根据待定系数法求得k、m的值，设设C点坐标为（a，），根据反比例函数与一次函数的交点问题解方程组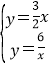可得到A点坐标为（2，3），B点坐标为（-2，-3），再利用待定系数法确定直线BC的解析式为y=，直线AC的解析式为y=-，于是利用y轴上点的坐标特征得到D点坐标为（0，-3），P点坐标为（0，+3），然后利用S△PBC=S△PBD+S△CPD得到关于a的方程，求出a的值即可得到C点坐标．

详解：∵点A的坐标为（2，3），

∴k=，m=6，

设BC交y轴于D，如图，设C点坐标为（a，）

解方程组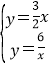得或，

∴A点坐标为（2，3），B点坐标为（-2，-3），

设直线BC的解析式为y=k′x+b，

把B（-2，-3）、C（a，）代入得 ，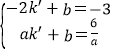

解得 ，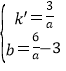

∴直线BC的解析式为y=，

当x=0时，y==，

∴D点坐标为（0，）

设直线AC的解析式为y=m′x+n，

把A（2，3）、C（a，）代入得，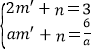

解得，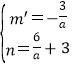

∴直线AC的解析式为y=-，

当x=0时，y=-=，

∴P点坐标为（0，）

∵S△PBC=S△PBD+S△CPD，

∴×2×6+×a×6=24，解得a=6，

∴C点坐标为（6，1）．

故选D．