题目内容
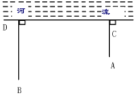
【题目】已知M＝（a＋24）x3﹣10x2＋10x＋5是关于x的二次多项式，且二次项系数和一次项系数分别为b和c，在数轴上A、B、C三点所对应的数分别是a、b、c．
（1）则a＝ ，b＝ ，c＝ ．
（2）有一动点P从点A出发，以每秒4个单位的速度向右运动，多少秒后，P到A、B、C的距离和为40个单位？
（3）在（2）的条件下，当点P移动到点B时立即掉头，速度不变，同时点T和点Q分别从点A和点C出发，向左运动，点T的速度1个单位/秒，点Q的速度5个单位/秒，设点P、Q、T所对应的数分别是xP、xQ、xT，点Q出发的时间为t，当
＜t＜
时，求2|xP﹣xT|＋|xT﹣xQ|＋2|xQ﹣xP|的值．
【答案】（1）﹣24，﹣10，10；（2）t＝2s或5s；（3）46
【解析】
（1）根据二次多项式的定义，列出方程求解即可；
（2）分三种情形，分别构建方程即可解决问题；
（3）当点P追上T的时间t1=
．当Q追上T的时间t2=
．当Q追上P的时间t3=
=20，推出当
＜t＜
时，位置如图，利用绝对值的性质即可解决问题.
（1）∵M＝（a＋24）x3﹣10x2＋10x＋5是关于x的二次多项式，
∴a＋24＝0，b＝﹣10，c＝10，∴a＝﹣24，
故答案为﹣24，﹣10，10．
（2）①当点P在线段AB上时，14＋（34﹣4t）＝40，解得t＝2．
②当点P在线段BC上时，34＋（4t﹣14）＝40，解得t＝5，
③当点P在AC的延长线上时，4t+（4t-14）+（4t-34）=40，解得t=
,不符合题意，排除，
∴t＝2s或5s时，P到A、B、C的距离和为40个单位．
（3）当点P追上T的时间t1=．
当Q追上T的时间t2=．
当Q追上P的时间t3==20，
∴当＜t＜时，位置如图，
∴2|xP﹣xT|＋|xT﹣xQ|＋2|xQ﹣xP|
＝2(3t－14)＋34－4t＋2(20－t)6t－28＋34－4t＋40－2t
＝74－28
＝46．
