题目内容
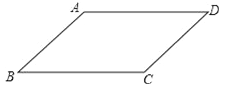
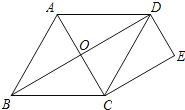
【题目】如图,在平行四边形BFEC中,连接FC,并延长至点D,延长CF至点A,使DC=AF,连接AB、DE.
(1)求证:AB∥DE.
(2)若平行四边形BFEC是菱形,且∠ABC=90°,AB=4,BC=3,则CF= .

【答案】(1)见解析;(2)3.6
【解析】
(1)根据平行四边形的性质得到BF∥CE,BF=CE,根据平行线的性质得到∠BFC=∠ECF,由平角的定义得到∠BFA=∠ECD,根据全等三角形的性质得到∠A=∠D,根据平行线的判定即可得到结论;
(2)过点B作BM⊥CF于点M,根据勾股定理得到AC=![]() =5,根据三角形的面积公式得到BM=
=5,根据三角形的面积公式得到BM=![]() =2.4,根据菱形的性质得到BF=BC=3,CF=2FM,根据勾股定理即可得到结论.
=2.4,根据菱形的性质得到BF=BC=3,CF=2FM,根据勾股定理即可得到结论.
(1)证明:∵四边形BFEC为平行四边形,
∴BF∥CE,BF=CE,
∴∠BFC=∠ECF,
∴∠BFA=∠ECD,
在△AFB与△DCE中, ,
,
∴△AFB≌△DCE,(SAS),
∴∠A=∠D,
∴AB∥DE;
(2)解:过点B作BM⊥CF于点M,
在Rt△ABC中,AC=![]() =5,
=5,
∵S△ABC=![]() ABBC=
ABBC=![]() ACBM,
ACBM,
∴BM=![]() =2.4,
=2.4,
又∵四边形BFEC为菱形,
∴BF=BC=3,CF=2FM,
在Rt△BFM中,FM=![]() =1.8,
=1.8,
∴CF=2×1.8=3.6.
故答案为:3.6.

练习册系列答案
相关题目