题目内容
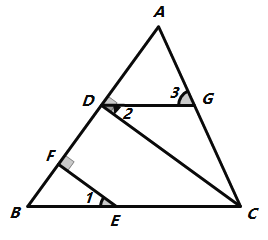
【题目】如图,在△ABC中,CD⊥AB,垂足为D. 点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
(1)试说明DG∥BC的理由;
(2)如果∠B=54°,且∠ACD=35°,求的∠3度数.
【答案】(1)见解析;(2)71°.
【解析】
(1)由CD⊥AB,EF⊥AB即可得出CD∥EF,从而得出∠1=∠BCD,再根据∠1=∠2即可得出∠2=∠BCD,依据“内错角相等,两直线平行”即可证出DG∥BC;
(2)在Rt△BCD中,利用直角三角形的两锐角互余可得到∠BCD的度数,进一步得到∠ACB,再根据BC∥DG即可得出∠3=∠ACB.
(1)证明:∵CD⊥AB,EF⊥AB,
∴∠BFE=∠BDC=90°,
∴CD∥EF,
∴∠1=∠BCD.
又∵∠1=∠2,
∴∠2=∠BCD,
∴DG∥BC.
(2)解:在Rt△BCD中,∠B=54°,
∴∠BCD=90°-54°=36°,
∴∠ACB=∠ACD+∠BCD=35°+36°=71°,
又∵BC∥DE,
∴∠3=∠ACB=71°.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目