题目内容
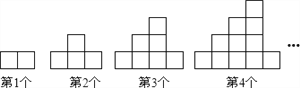
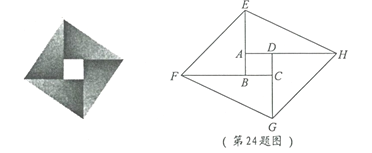
【题目】如图，将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内（相邻纸片之间互不重叠也无缝隙），未被四张正方形纸片覆盖的部分用阴影表示，设右上角与左下角阴影部分的周长的差为l．若知道l的值，则不需要测量就能知道周长的正方形的标号为（ ）
A.①B.②C.③D.④
【答案】D
【解析】
设①、②、③、④四个正方形的边长分别为a、b、c、d，用a、b、c、d表示出右上角、左下角阴影部分的周长，利用整式的加减混合运算法则计算，得到答案．
设①、②、③、④四个正方形的边长分别为a、b、c、d，
由题意得，（a+d-b-c+b+a+d-b+b-c+c+c）-（a-d+a-d+d+d）=l，
整理得，2d=l，
则知道l的值，则不需测量就能知道正方形④的周长，
故选D．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
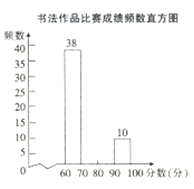
【题目】我市举行“第十七届中小学生书法大赛”作品比赛，已知每幅参赛作品成绩记为
，组委会从1000幅书法作品中随机抽取了部分参赛作品，统计了它们的成绩，并绘制成如下统计图表.
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
| ______ | 0.32 |
| ______ | ______ |
| 10 | 0.1 |
合计 | ______ | 1 |
根据上述信息，解答下列问题：
(1)请你把表中的数据填写完整.
(2)补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖，试估计全市获得等级奖的幅数.
