题目内容
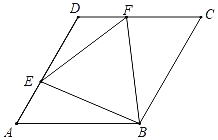
【题目】如图,菱形ABCD的边长为4,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,AE+CF=4,则△BEF面积的最小值为_____.
【答案】3![]() .
.
【解析】
首先证明△BEF是等边三角形,当BE⊥AD时面积最小.
连接BD,
∵菱形ABCD边长为4,∠BAD=60°;
∴△ABD与△BCD为正三角形,
∴∠FDB=∠EAB=60°,
∵AE+CF=4,DF+CF=4,
∴AE=DF,
∵AB=BD,
∴△BDF≌△BAE(SAS),
∴BE=BF,
∠ABE=∠DBF,
∴∠EBF=∠ABD=60°,
∴△BEF是等边三角形,
∴当BE⊥AD时,△BEF的面积最小,此时BE=![]() ,
,
∴边BE上的高为![]() =3,
=3,
△BEF面积的最小值=![]() .
.
故答案为![]() .
.


练习册系列答案
相关题目