题目内容
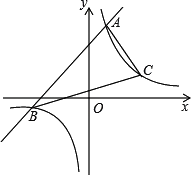
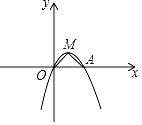
【题目】如图,在平面直角坐标系中,顶点为M的抛物线C:y=ax2+bx与x轴的另一个交点为A(2,0),连接OM、AM,∠OMA=90°.
(1)求抛物线C1的函数表达式;
(2)已知点D的坐标为(0,﹣2),将抛物线C1向上平移得到抛物线C2,抛物线C2与x轴分别交于点E、F(点E在点F的左侧),如果△DOM与△MAF相似,求所有符合条件的抛物线C2的函数表达式.
【答案】(1)y=﹣x2+2x;(2)y=(x﹣1)2+9或y=﹣(x﹣1)2+4.
【解析】
(1)过M作MH⊥![]() 轴于H,可得OH=AH=MH=
轴于H,可得OH=AH=MH=![]() OA=1,则M(1,1),把点A(2,0)、M(1,1)代入y=ax2+bx可解得
OA=1,则M(1,1),把点A(2,0)、M(1,1)代入y=ax2+bx可解得![]() ,则抛物线C1的函数表达式为y=﹣x2+2x;
,则抛物线C1的函数表达式为y=﹣x2+2x;
(2)分两种情况讨论:①当△MOD∽△MAF时,![]() ,即
,即![]() ,解得AF=2,则F(4,0);②当△MOD∽△FAM时,
,解得AF=2,则F(4,0);②当△MOD∽△FAM时, ![]() ,即
,即![]() ,解得AF=1.则F(3,0).设抛物线C2的函数表达式为
,解得AF=1.则F(3,0).设抛物线C2的函数表达式为![]() .把点F(4.0)、F.(3.0)分别代入得m=9,m=4.从而求出符合条件的抛物线C2的函数表达式为
.把点F(4.0)、F.(3.0)分别代入得m=9,m=4.从而求出符合条件的抛物线C2的函数表达式为![]() 或
或![]() .
.
解:(1)由抛物线的对称性可得:OM=AM.
∵∠OMA=90°,
∴△OMA是等腰直角三角形,
过M作MH⊥工轴于H,
可得OH=AH=MH=![]() OA=1.
OA=1.
∴M(1,1),
把点A(2,0)、M(1,1)代入y=ax2+bx,可得
![]() ,
,
解得![]() ,
,
∴抛物线C1的函数表达式为y=﹣x2+2x.
(2)∵△OMA是等腰直角三角形,
∴∠MOA=∠MAO=45°,OM=AM=![]() ,
,
∴MOD=∠MOA+∠AOD=135°=∠MAF.
①当△MOD∽△MAF时,
![]() ,
,
即![]()
解得AF=2,
∴F(4,0);
②当△MOD∽△FAM时,
![]() ,
,
即![]() ,
,
解得AF=1.
∴F(3,0).
∵抛物线C1向上平移得到抛物线C2,
∴设抛物线C2的函数表达式为![]() .
.
把点F(4.0)、F.(3.0)分别代入得m=9,m=4.
综上,所有符合条件的抛物线C2的函数表达式为![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?