题目内容
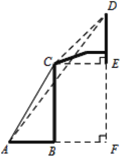
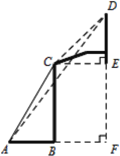
【题目】如图所示,一副篮架由配重、支架、篮板与篮筐组成,在立柱的C点观察篮板上沿D点的仰角为45°,在支架底端的A点观察篮板上沿D点的仰角为54°,点C与篮板下沿点E在同一水平线,若AB=1.91米,篮板高度DE为1.05米,求篮板下沿E点与地面的距离.(结果精确到0.1m,参考数据:sin54°≈0.80, cos54°≈0.60,tan54°≈1.33)

【答案】篮板下沿E点沿与地面的距离为2.9米.
【解析】
过D作DF⊥AB的延长线于F,连接CE,根据题目已知条件可以得到CE=DE=1.05,四边形CBFE为矩形,利用矩形的性质CE=BF=1.05,最后利用解直角三角形即可得出结果.
解:如图所示,过D作DF⊥AB的延长线于F,连接CE.
在Rt△DEC中,∠DCE=45°,DE=1.05(米),
∴CE=DE=1.05(米),
∵∠CBF=∠F=∠CEF=90°,
∴四边形CBFE为矩形,
∴CE=BF=1.05(米),
∴AF=AB+BF=2.96(米),
在Rt△AFD中,AF=2.96(米),∠DAF=54°,
由DF=AF·tan54°得DF≈3.94(米),
∴EF=3.94-1.05≈2.9(米).
答:篮板下沿E点沿与地面的距离为2.9米.

 阅读快车系列答案
阅读快车系列答案【题目】为普及防治新型冠状病毒感染的科学知识和有效方法,不断增强同学们的自我保护意识,学校举办了新型冠状病毒疫情防控网络知识竞答活动,试卷题目共10题,每题10分.现分别从七年级的三个班中各随机取10名同学的成绩(单位:分),收集数据如表:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 | a | 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | |
2班 | 83 | c | d |
3班 | b | 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中a,b,c,d的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;
(3)为了让同学们重视疫情防控知识的学习,学校将给竞答成绩满分的同学颁发奖状,该校七年级新生共600人,试估计需要准备多少张奖状?