Question

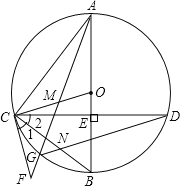
【题目】在图1至图3中，的直径，切于点，，连接交于点，连接，是线段上一点，连接．

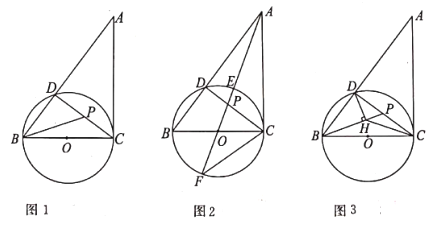
（1）如图1，当点，的距离最小时，求的长；

（2）如图2，若射线过圆心，交于点，，求的值；

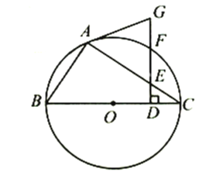
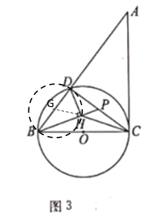
（3）如图3，作于点，连接，直接写出的最小值．

Answer 1

【答案】（1）12；（2）；（3）的最小值为

【解析】

（1）连接，根据切线的性质和圆周角定理的推论可得,∠BDC=90°，利用勾股定理求出AB，然后根据三角形的面积公式即可求出CD，根据垂线段最短可得当时，点，的距离最小，从而求出PD的长；

（2）连接，则，利用勾股定理即可求出AE，然后根据相似三角形的判定定理证出，列出比例式，根据正切的定义即可求出结论；

（3）以 为直径作，则为的中点，利用勾股定理和圆的基本性质求出半径DG，根据直径所对的圆周角是直角可得点H一定在上，当点，，在一条直线上时，最小，利用勾股定理求出CG，即可求出结论．

解：（1）如图1，连接，

切于点，BC为直径

,∠BDC=90°

，，

．

由,

即,

解得，

当时，点，的距离最小，此时．

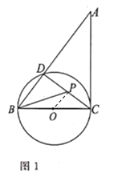
（2）如图2，连接，则．

由（1）知，，

由，

得，

解得．

，

．

又，

，

．

．

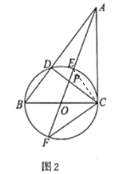
（3）的最小值为．

如图3，以 为直径作，则为的中点，

BD=

∴，

，

∴点总在上，，

∴当点，，在一条直线上时，最小，

此时，，

，

即的最小值为．