题目内容
【题目】如图,在边长为6的等边△ABC中,AD是BC边上的中线,点E是△ABC内一个动点,且DE=2,将线段AE绕点A逆时针旋转60°得到AF,则DF的最小值是______.

【答案】![]()
【解析】
以ED为边作等边△DEG,连接AD,EF,AG,由等边三角形的性质和勾股定理可求AD=3![]() ,由等边三角形的性质可证△AEG≌△FED,可得DF=AG,根据三角形的三边关系,可得当点A,点G,点D三点共线时,AG值最小,即DF值最小,则可求线段DF的最小值.
,由等边三角形的性质可证△AEG≌△FED,可得DF=AG,根据三角形的三边关系,可得当点A,点G,点D三点共线时,AG值最小,即DF值最小,则可求线段DF的最小值.
如图,以ED为边作等边△DEG,连接AD,EF,AG,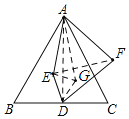
∵△ABC是等边三角形,点D是BC中点,
∴BD=CD=3,AD⊥BC,
∴AD=![]() =3
=3![]() ,
,
∵将线段AE绕点A逆时针旋转60°得AF,
∴AE=AF,∠EAF=60°,
∴△AEF是等边三角形,
∴AE=EF,∠AEF=60°,
∵△DEG是等边三角形,
∴DE=EG=2,∠GED=60°=∠AEF,
∴∠AEG=∠FED,且AE=EF,EG=DE,
∴△AEG≌△FED(SAS),
∴DF=AG,
∵在△ADG中,AG≥AD-DG,
∴当点A,点G,点D三点共线时,AG值最小,即DF值最小,
∴DF最小值=AD-DG=3![]() -2.
-2.
故答案为:3![]() -2.
-2.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】某工厂生产一种合金薄板(其厚度忽略不计)这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,(即出厂价=基础价+浮动价)其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长x成正比例,在营销过程中得到了表格中的数据,已知出厂一张边长为40cm的薄板,获得利润是26元.(利润=出厂价-成本价)
薄板的边长(cm) | 20 | 30 |
出厂价(元/张) | 50 | 70 |
(1)求一张薄板的出厂价y与边长x之间满足的函数关系式;
(2)求一张薄板的利润p与边长x之间的函数关系式;
(3)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?当薄板的边长为多少时,所获利润最大,求出这个最大值。