题目内容
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象在第一象限交于点
的图象在第一象限交于点![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,且
,且![]() .
.

(1)求一次函数![]() 和
和![]() 的表达式;
的表达式;
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 是以
是以![]() 为腰的等腰三角形,若存在,求出点
为腰的等腰三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)反比例函数![]() 的图象记为曲线
的图象记为曲线![]() ,将
,将![]() 向右平移3个单位长度,得曲线
向右平移3个单位长度,得曲线![]() ,则
,则![]() 平移至
平移至![]() 处所扫过的面积是_________.(直接写出答案)
处所扫过的面积是_________.(直接写出答案)
【答案】(1)反比例函数解析式为![]() ;一次函数的解析式为y=2x-5;(2)存在,
;一次函数的解析式为y=2x-5;(2)存在,![]() ,
,![]() ,
,![]() ,
,![]() ;(3)27
;(3)27
【解析】
(1)把点A的坐标代入反比例函数解析式,求出a,根据勾股定理求出OA,得到OB的长,求出点B的坐标,利用待定系数法求出一次函数解析式;
(2)根据勾股定理求出AB,分AB=AC、BC=AB两种情况,根据勾股定理列方程计算,得到答案;
(3)分别把x=1、x=4代入反比例函数解析式求出函数值,求出平行四边形EFNM的面积,求出C1平移至C2处所扫过的面积.
解:(1)∵点A(4,3)在反比例函数![]() 的图象上,
的图象上,
∴a=4×3=12,
∴反比例函数解析式为![]() ;
;
∵![]() ,OA=OB,点B在y轴负半轴上,
,OA=OB,点B在y轴负半轴上,
∴点B(0,-5).
把点A(4,3)、B(0,-5)代入y=kx+b中,
得:![]() ,解得:
,解得:![]() ,
,
∴一次函数的解析式为y=2x-5.
(2)存在,
∵点A(4,3),点B(0,-5)
∴![]()
设点C的坐标为(m,0),
①△ABC为等腰三角形,
当![]() 时,
时,
则![]()
∴![]() ,
,![]()
∴C的坐标为![]() 或
或![]()
②当![]() 时,
时,
则![]()
∴![]() ,
,![]()
∴C的坐标为![]() 或
或![]()
综上所述:![]() ,
,![]() ,
,![]() ,
,![]()
(3)设点E的横坐标为1,点F的横坐标为4,点M、N分别对应点E、F,如图所示.
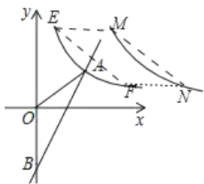
令![]() 中x=1,则y=12,
中x=1,则y=12,
∴E(1,12);
令![]() 中x=4,则y=3,
中x=4,则y=3,
∴F(4,3),
∵EM∥FN,且EM=FN,
∴四边形EMNF为平行四边形,
∴S=EM(yEyF)=3×(123)=27.
C1平移至C2处所扫过的面积正好为平行四边形EMNF的面积.
故答案为:27.

【题目】为普及防治新型冠状病毒感染的科学知识和有效方法,不断增强同学们的自我保护意识,学校举办了新型冠状病毒疫情防控网络知识竞答活动,试卷题目共10题,每题10分.现分别从七年级的三个班中各随机取10名同学的成绩(单位:分),收集数据如表:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 | a | 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | |
2班 | 83 | c | d |
3班 | b | 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中a,b,c,d的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;
(3)为了让同学们重视疫情防控知识的学习,学校将给竞答成绩满分的同学颁发奖状,该校七年级新生共600人,试估计需要准备多少张奖状?