题目内容
【题目】已知二次函数![]() .
.
(1)求证这个二次函数的图像一定与x轴有交点;
(2)若这个二次函数有最大值0,求m的值;
(3)我们定义:若二次函数![]() 的图像与x轴正半轴的两个交点的横坐标
的图像与x轴正半轴的两个交点的横坐标![]() ,满足2<
,满足2<![]() <3,则称这个二次函数与x轴有两个“黄金交点”.如果二次函数
<3,则称这个二次函数与x轴有两个“黄金交点”.如果二次函数![]() 与x轴有两个“黄金交点”,求m的取值范围.
与x轴有两个“黄金交点”,求m的取值范围.
【答案】(1)图像与x轴有交点;(2)m=-1;(3)![]() 或
或![]()
【解析】
(1)当b2-4ac>0,图象与x轴有两个交点;当b2-4ac=0,图象与x轴有一个交点;当b2-4ac<0,图象与x轴没有交点.
(2)二次函数有最大值,说明抛物线开口向下;二次函数有最大值0,说明抛物线与x轴只有一个交点,即可求解.
(3)抛物线与x轴的交点纵坐标都等于0,根据![]() ,解得:x1=1,x2=
,解得:x1=1,x2=![]() ,最后分情况讨论即可.
,最后分情况讨论即可.
(1)∵b2-4ac=(m+1)2≥0
∴图像与x轴有交点
(2)∵二次函数有最大值
∴m![]() 0
0
∵二次函数有最大值0
∴b2-4ac=(m+1)2=0
∴m=-1
(3)解方程![]()
得:x1=1,x2=![]() 可得m
可得m![]() 0
0
①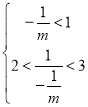 解得:
解得:![]()
②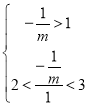 解得:
解得:![]()

练习册系列答案
相关题目