题目内容
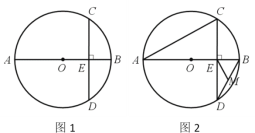
【题目】已知AB是⊙O的直径,C是⊙O上的一点(不与点A,B重合),过点C作AB的垂线交⊙O于点D,垂足为E点.
(1)如图1,当AE=4,BE=2时,求CD的长度;
(2)如图2,连接AC,BD,点M为BD的中点.求证:ME⊥AC.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)先求出半径,然后利用勾股定理求出CE的长度,最后利用垂径定理即可求出CD的长度;
(2)延长ME与AC交于点N,先利用直角三角形斜边中线的性质和等腰三角形的性质得出∠CEN=∠DEM=∠D,然后利用∠B=∠C,![]() 得出
得出![]() ,则∠CNE =90°,则结论可证.
,则∠CNE =90°,则结论可证.
解:(1)如图1,连接OC.
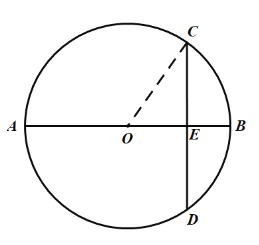
∵ AE=4,BE=2,
∴AB =6,
∴CO =AO=3,
∴OE =AE-AO=1,
∵CD⊥AB,
∴ CE=![]()
∵AB是⊙O的直径,CD⊥AB,
∴CE=DE,
∴ CD=2CE=![]() .
.
(2)证明:如图2,延长ME与AC交于点N.
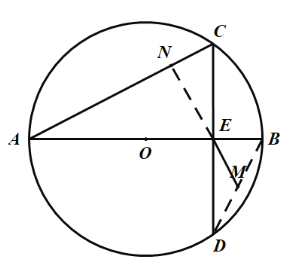
∵CD⊥AB,
∴∠BED=90°.
∵ M为BD中点,
∴EM =![]() BD =DM,
BD =DM,
∴∠DEM=∠D,
∴∠CEN=∠DEM=∠D.
∵∠B=∠C,![]()
![]()
∴∠CNE =90°,
即ME⊥AB.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目