题目内容
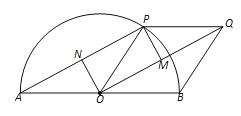
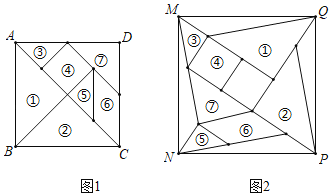
【题目】七巧板是我国祖先的一项卓越创造，如图正方形ABCD可以制作一副七巧板，现将这副七巧板拼成如图2的“风车”造型（内部有一块空心），连结最外围的风车顶点M、N、P、Q得到一个四边形MNPQ，则正方形ABCD与四边形MNPQ的面积之比为（ ）
A.5：8B.3：5C.8：13D.25：49
【答案】C
【解析】
本题主要是勾股定理的应用，关键是找出两个正方形的边长，与他们边长有关的是图1的对角线AC，图2中的边可以转化到ME，EQ两条边上，统一用相同的字母设出来，然后代入勾股定理公式计算即可．
解：设AC＝a+a+a+a＝4a，则AB＝BC＝AC×sin45°＝2
a，
所以正方形ABCD的面积是（2 a）2＝8a2；
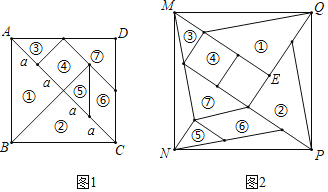
图2中ME＝3a，EQ＝2a，
由勾股定理得：MQ＝
＝
a，
所以正方形MNPQ的面积为（ a）2＝13a2，
所以图中正方形ABCD，MNPQ的面积比为 
=
，
故选：C．
练习册系列答案
相关题目
