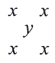Question

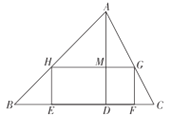
【题目】在等腰梯形ABCD中，AD∥BC，AB=DC=5，AD=6，BC=12．

（1）梯形ABCD的面积等于 ．

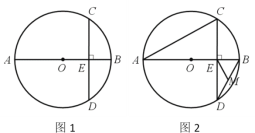
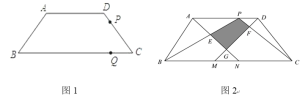
（2）如图1，动点P从D点出发沿DC以DC以每秒1个单位的速度向终点C运动，动点Q从C点出发沿CB以每秒2个单位的速度向B点运动．两点同时出发，当P点到达C点时，Q点随之停止运动．当PQ∥AB时，P点离开D点多少时间？

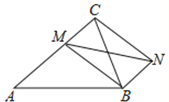
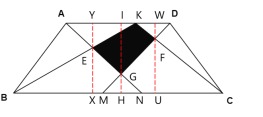
（3）如图2，点K是线段AD上的点，M、N为边BC上的点，BM=CN=5，连接AN、DM，分别交BK、CK于点E、F，记△ ADG和△ BKC重叠部分的面积为S，求S的最大值．

Answer 1

【答案】（1）36；（2）t=；（3）

【解析】

（1）已知梯形各边的长，用勾股定理易求高以及其面积；

（2）本题要找出线段之比，设要用x秒后PQ∥AB，已知，求出x的值即可；

（3）过G作GH⊥BC，延长HG交AD于I；过E作EX⊥BC，延长XE交AD于Y；过F作FU⊥BC，延长UF交AD于W；利用相似三角形的性质分别表示出EX和FU的长，再利用得到相应的关系式，最后通过配方求得S的最大值即可．

解：（1）如图，过点D作DE⊥BC于点E，

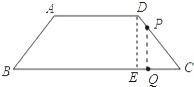
∵AB＝DC＝5，AD＝6，BC＝12．

∴由题意可知CE＝（BC-AD）＝3，

在Rt△DEC中，，

∴梯形ABCD的面积为，

故答案为：36；

（2）分别延长BA和CD，交于点N，

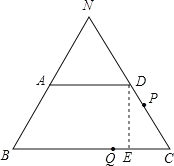
则NA：NB＝AD：BC，即

NA＝5，则ND＝NA＝5．

设用了x秒PQ∥AB，则DP＝x，PC＝5－x，CQ＝2x．

PC：CN＝CQ：CB，

，x＝．

即当PQ∥AB时，P点离开D点的时间等于秒；

（3）过G作GH⊥BC，延长HG交AD于I；

过E作EX⊥BC，延长XE交AD于Y；

过F作FU⊥BC，延长UF交AD于W；

∵AD∥BC，

∴△MGN∽△DGA，

∴ ，

∴HG＝1，

设AK＝x，

∵AD∥BC，

∴△BEN∽△KEA，

∴，

∴，

同理：，

∴

∴当x＝3时，