题目内容
【题目】如图,在四边形![]() 中,已知
中,已知![]() ,
,![]() .
.
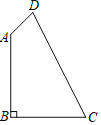
(1)求![]() 的度数;
的度数;
(2)求四边形![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由于∠B=90°,AB=BC=2,利用勾股定理可求AC,并可求∠BAC=45°,而CD=3,DA=1,易得AC2+DA2=CD2,可证△ACD是直角三角形,于是有∠CAD=90°,从而易求∠BAD;
(2)连接AC,则可以计算△ABC的面积,根据AB、BC可以计算AC的长,根据AC,AD,CD可以判定△ACD为直角三角形,根据AD,CD可以计算△ACD的面积,四边形ABCD的面积为△ABC和△ADC面积之和.
(1)连结AC,
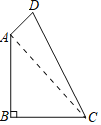
∵∠B=90°,AB=BC=2,
∴AC=2![]() ,∠BAC=45°,
,∠BAC=45°,
∵AD=1,CD=3,
∴AD2+AC2=12+(2![]() )2=9,CD2=9,
)2=9,CD2=9,
∴AD2+AC2=CD2,
∴△ADC是直角三角形,
∴∠DAC=90°,
∴∠DAB=∠DAC+∠BAC=135°.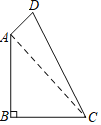
(2)在 Rt△ABC中,S△ABC=![]() BCAB=
BCAB=![]() ×2×2=2,
×2×2=2,
在 Rt△ADC中,S△ADC=![]() ADAC=
ADAC=![]() ×1×2
×1×2![]() =
=![]() .
.
∴S四边形ABCD=S△ABC+S△ADC=2+![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目