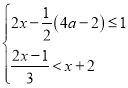题目内容
【题目】对任意一个正整数m,如果m=k(k+1),其中k是正整数,则称m为“矩数”,k 为m的最佳拆分点.例如,56=7×(7+1),则56是一个“矩数”,7为56的最佳拆分点.
(1)求证:若“矩数”m是3的倍数,则m一定是6的倍数;
(2)把“矩数”p与“矩数”q的差记为 D(p,q),其中p>q,D(p,q)>0.例如,20=4×5,6=2×3,则 D(20,6)=20﹣6=14.若“矩数”p的最佳拆分点为t,“矩数”q的最佳拆分点为s,当 D(p,q)=30时,求 ![]() 的最大值.
的最大值.
【答案】
(1)证明:若“矩数”m=k(k+1)是3的倍数,则k(k+1)是3的倍数,k是正整数,
当k为奇数时,k+1是偶数,则k(k+1)是能被3整除的偶数,故k(k+1)是6的倍数;
当k为偶数时,则k(k+1)是能被3整除的偶数,故k(k+1)是6的倍数,
综上所述,若“矩数”m是3的倍数,则m一定是6的倍数
(2)解:根据题意得p=t(t+1),q=s(s+1),D(p,q)=t(t+1)﹣s(s+1)=30,
即t2+t﹣s2﹣s=30,
∴(t﹣s)(t+s+1)=30,
∵t,s是正整数,t>s,
∴t﹣s,t+s+1是正整数,且t+s+1>t﹣s,
∵30=1×30=2×15=3×10=5×6,
∴ ![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() ,
,
解得: ![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() ,
,
∵t,s是正整数,
∴符合条件的是: ![]() 或
或 ![]() 或
或 ![]() ,
,
∴ ![]() 或
或 ![]() =
= ![]() 或
或 ![]() =
= ![]() ,
,
∵ ![]() ,
,
∴ ![]() 的最大值是
的最大值是 ![]()
【解析】(1)连续的两个整数必是一奇数,一偶数,可分类证明;(2)可把新定义的规则转化为已知的规则,用已知代数式表示新运算法则,根据30的因数分解规则,求出最大值.
【考点精析】解答此题的关键在于理解因式分解的应用的相关知识,掌握因式分解是整式乘法的逆向变形,可以应用与数字计算、求值、整除性问题、判断三角形的形状、解方程.

 名校课堂系列答案
名校课堂系列答案【题目】二次函数 ![]() ,自变量x与函数y的对应值如下表:
,自变量x与函数y的对应值如下表:
x | … | -5 | -4 | -3 | -2 | -1 | 0 | … |
y | … | 4 | 0 | -2 | -2 | 0 | 4 | … |
下列说法正确的是( )
A.抛物线的开口向下
B.当x>-3时,y随x的增大而增大
C.二次函数的最小值是-2
D.抛物线的对称轴x= ![]()