题目内容
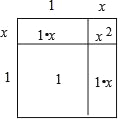
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)图1中阴影部分面积为______,图2中阴影部分面积为_____,对照两个图形的面积可以验证________公式(填公式名称)请写出这个乘法公式________.
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.

【答案】(1) a2﹣b2,(a+b)(a﹣b),平方差,a2﹣b2=(a+b)(a﹣b);(2)①5;②2128.
【解析】
(1)根据两个图形中阴影部分的面积相等,即可列出等式;
(2)①把x2﹣4y2利用(1)的结论写成两个式子相乘的形式,然后把x+2y=4代入即可求解;
②利用平方差公式化成式子相乘的形式即可求解.
解:(1)图1中阴影部分面积为a2﹣b2,图2中阴影部分面积为(a+b)(a﹣b),
对照两个图形的面积可以验证平方差公式:a2﹣b2=(a+b)(a﹣b).
故答案为:a2﹣b2,(a+b)(a﹣b),平方差,a2﹣b2=(a+b)(a﹣b).
(2)①∵x2﹣4y2=(x+2y)(x﹣2y),
∴15=3(x﹣2y),
∴x﹣2y=5;
②(2+1)(22+1)(24+1)(28+1)……(264+1)+1
=(2﹣1)(2+1)(22+1)(24+1)(28+1)……(264+1)+1
=(22﹣1)(22+1)(24+1)(28+1)……(264+1)+1
=(24﹣1)(24+1)(28+1)……(264+1)+1
=(28﹣1)(28+1)……(264+1)+1
=(264﹣1)(264+1)+1
=2128﹣1+1
=2128.

 轻松暑假总复习系列答案
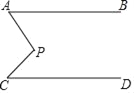
轻松暑假总复习系列答案【题目】如图,AB∥CD,∠A=50°,∠C=45°,求∠P的度数.
下面提供三种思路:
(1)过P作FG∥AB
(2)延长AP交直线CD于M;
(3)延长CP交直线AB于N.
请选择两种思路,求出∠P的度数.