题目内容
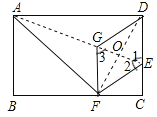
【题目】如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG.

(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求![]() 的值.
的值.
【答案】(1)证明见试题解析;(2)![]() .
.
【解析】试题分析:(1)由折叠的性质,可以得到DG=FG,ED=EF,∠1=∠2,由FG∥CD,可得∠1=∠3,再证明 FG=FE,即可得到四边形DEFG为菱形;
(2)在Rt△EFC中,用勾股定理列方程即可CD、CE,从而求出![]() 的值.
的值.
试题解析:(1)由折叠的性质可知:DG=FG,ED=EF,∠1=∠2,∵FG∥CD,∴∠2=∠3,∴FG=FE,∴DG=GF=EF=DE,∴四边形DEFG为菱形;
(2)设DE=x,根据折叠的性质,EF=DE=x,EC=8﹣x,在Rt△EFC中,![]() ,即
,即![]() ,解得:x=5,CE=8﹣x=3,∴
,解得:x=5,CE=8﹣x=3,∴![]() =
=![]() .
.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目