题目内容
【题目】如图,在直角坐标系中,四边形OABC为矩形,A(6,0),C(0,3),点M在边OA上,且M(4,0),P、Q两点同时从点M出发,点P沿x轴向右运动;点Q沿x轴先向左运动至原点O后,再向右运动到点M停止,点P随之停止运动.P、Q两点运动的速度分别为每秒1个单位、每秒2个单位.以PQ为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与矩形OABC重叠部分(阴影部分)的面积为S(平方单位).
(1)用含t的代数式表示点P的坐标.
(2)分别求当t=1,t=3时,线段PQ的长.
(3)求S与t之间的函数关系式.
(4)直接写出L落在第一象限的角平分线上时t的值.

【答案】(1)P(4+t,0)(0≤t≤4);(2)当t=1时, PQ=3,当t=3时, PQ=5;(3)S=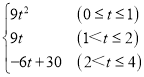 ;(4)t=
;(4)t=![]() 或
或![]() s时,L落在第一象限的角平分线上.
s时,L落在第一象限的角平分线上.
【解析】
(1)求出OP的长即可解决问题;
(2)法两种情形分别求出MQ、PM的长即可解决问题;
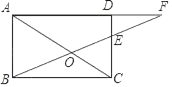
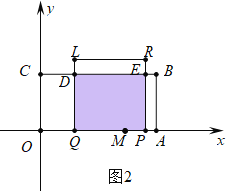
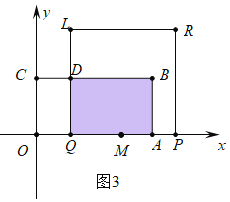
(3)法三种情形:①如图1中,当0≤t≤1时,重叠部分是正方形PQLR;②如图2中,当1<t≤2时,重叠部分是四边形PQDE;③如图3中,当2<t≤4时,重叠部分是四边形ABDQ,分别求解即可;
(4)根据OQ=PQ,构建方程即可解决问题.
解:(1)如图1中,∵M(4,0),
∴OM=4.PM=t,
∴OP=4+t,
∴P(4+t,0)(0≤t≤4).
(2)当t=1时,MQ=2,MP=1,
∴PQ=3.
当t=3时,MQ=2,PM=3,
∴PQ=2+3=5.
(3)①如图1中,当0≤t≤1时,重叠部分是正方形PQLR,S=PQ2=9t2

②如图2中,当1<t≤2时,重叠部分是四边形PQDE,S=PQDQ=9t.
③如图3中,当2<t≤4时,重叠部分是四边形ABDQ,S=AQAB=3[6-2(t-2)]=-6t+30.
综上所述,S=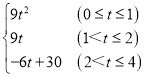 .
.
(4)L落在第一象限的角平分线上时,OQ=LQ=PQ,
∴4-2t=3t或2(t-2)=t+4-2(t-2),
解得t=![]() 或
或![]() .
.
∴t=![]() 或
或![]() s时,L落在第一象限的角平分线上.
s时,L落在第一象限的角平分线上.

 名校课堂系列答案
名校课堂系列答案