题目内容
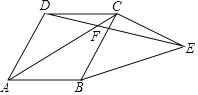
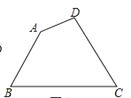
【题目】如图，现有一块四边形的木板余料ABCD，经测量AB=25cm，BC=54cm，CD=30cm，且tanB=tanC=
，木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN，则该矩形的面积为____________．
【答案】486
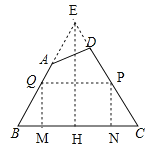
【解析】解： 如图，延长BA、CD交于点E，过点E作EH⊥BC于点H．∵∠B=∠C，∴EB=EC．∵BC=54cm，且EH⊥BC，∴BH=CH=
BC=27cm．∵tanB=
=
，∴EH=36cm．在Rt△BHE中，BE=
=45cm．∵AB=25cm，∴AE=20cm，∴BE的中点Q在线段AB上．∵CD=30cm，∴ED=15cm，∴CE的中点P在线段CD上，∴中位线PQ的两端点在线段AB、CD上．设PN=x，矩形PQMN的面积为S，由条件可得△EQP∽△EBC，∴
，解得： QP=54﹣1.5x．则S=PNPQ=x（54﹣1.5x）=
=
，故S的最大值为486．故答案为：486．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
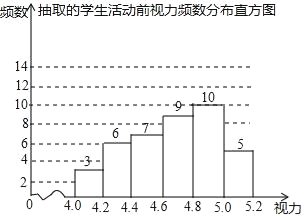
【题目】为了保护视力，学校开展了全校性的视力保健活动，活动前，随机抽取部分学生，检查他们的视力，结果如图所示（数据包括左端点不包括右端点，精确到0.1）；活动后，再次检查这部分学生的视力，结果如表所示
分组 | 频数 |
4.0≤x＜4.2 | 2 |
4.2≤x＜4.4 | 3 |
4.4≤x＜4.6 | 5 |
4.6≤x＜4.8 | 8 |
4.8≤x＜5.0 | 17 |
5.0≤x＜5.2 | 5 |
（1）求活动所抽取的学生人数；
（2）若视力达到4.8及以上为达标，计算活动前该校学生的视力达标率；
（3）请选择适当的统计量，从两个不同的角度评价视力保健活动的效果．
