题目内容
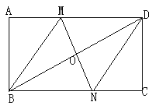
【题目】如图所示,矩形ABCD中,点E在DC上且DE:EC=2:3,连接BE交对角线AC于点O.延长AD交BE的延长线于点F,则△AOF与△BOC的面积之比为( )
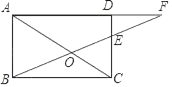
A. 9:4B. 3:2C. 25:9D. 16:9
【答案】C
【解析】
由矩形的性质可知:AB=CD,AB∥CD,进而可证明△AOB∽△COE,结合已知条件可得AO:OC=3:5,再根据相似三角形的性质:面积之比等于相似比的平方即可求出△AOF与△BOC的面积之比.
解:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,
∴△AOB∽△COE,
∵DE:EC=2:3,
∴CE:CD=3:5,
∴CE:CD=CE:AB=CO:AO=3:5,
∴S△AOF:S△BOC=25:9.
故选:C.

练习册系列答案
相关题目