题目内容
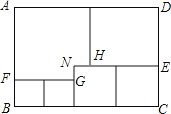
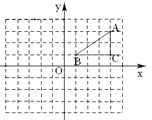
【题目】如图 , ![]() 中,
中, ![]() ,线段
,线段![]() 在射线
在射线![]() 上,且
上,且![]() ,线段
,线段![]() 沿射线
沿射线![]() 运动,开始时,点
运动,开始时,点![]() 与点
与点![]() 重合,点
重合,点![]() 到达点
到达点![]() 时运动停止,过点
时运动停止,过点![]() 作
作![]() ,与射线
,与射线![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 的垂线,与射线
的垂线,与射线![]() 相交于点
相交于点![]() .设
.设![]() ,四边形
,四边形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() 关于
关于![]() 的函数图象如图所示(其中
的函数图象如图所示(其中![]() 时,函数的解析式不同)
时,函数的解析式不同)
(1)填空: ![]() 的长是 ;
的长是 ;
(2)求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围.
的取值范围.

【答案】(1)6;(2)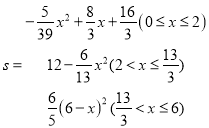
【解析】试题分析:(1)由图象即可解决问题.
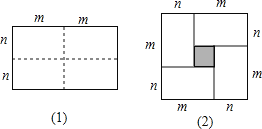
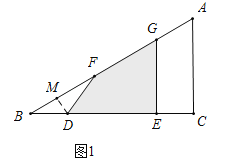
(2)分三种情形①如图1中,当0≤x≤2时,作DM⊥AB于M,根据S=S△BEG﹣S△BDF即可解决.
②如图2中,作AN∥DF交BC于N,设BN=AN=x.在Rt△ANC中,利用勾股定理求出x,再根据S= S△ABC﹣S△BDF即可解决.
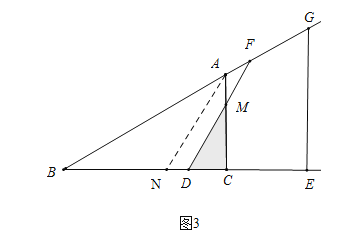
③如图3中,根据S=![]() CDCM,求出CM即可解决问题.
CDCM,求出CM即可解决问题.
试题解析:解;(1)由图象可知BC=6.故答案为:6.
(2)①如图1中,当0≤x≤2时,作DM⊥AB于M,由题意BC=6,AC=4,∠C=90°,∴AB=![]() =
=![]() .∵∠B=∠B,∠DMB=∠C=90°,∴△BMD∽△BCA,∴
.∵∠B=∠B,∠DMB=∠C=90°,∴△BMD∽△BCA,∴![]() ,∴DM=
,∴DM=![]() ,BM=
,BM=![]() .∵BD=DF,DM⊥BF,∴BM=MF,∴S△BDF=
.∵BD=DF,DM⊥BF,∴BM=MF,∴S△BDF=![]() .∵EG∥AC,∴
.∵EG∥AC,∴![]() ,∴
,∴![]() ,∴EG=
,∴EG=![]() (x+4),∴S=S△BEG﹣S△BDF=
(x+4),∴S=S△BEG﹣S△BDF=![]() =
=![]() .
.
②如图②中,作AN∥DF交BC于N,设BN=AN=x.在Rt△ANC中,∵AN2=CN2+AC2,∴x2=42+(6﹣x)2,∴x=![]() ,∴当2<x≤
,∴当2<x≤![]() 时,S=S△ABC﹣S△BDF=12﹣
时,S=S△ABC﹣S△BDF=12﹣![]() ;
;

③如图3中,当![]() <x≤6时.∵DM∥AN,∴
<x≤6时.∵DM∥AN,∴![]() ,∴
,∴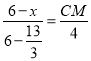 ,∴CM=
,∴CM=![]() (6﹣x),∴S=
(6﹣x),∴S=![]() CDCM=
CDCM=![]() .
.
综上所述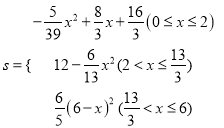 .
.

 阅读快车系列答案
阅读快车系列答案【题目】某班同学为了解2019年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行整理如下:
月均用水量x(t) | 频数(户) | 频率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
| 2 | 0.04 |

请解答下列问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?