题目内容
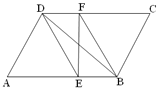
【题目】已知:如图,在□ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=600,AE=2EB,AD=4,求四边形DEBF的周长和面积.
【答案】(1)证明见解析;(2)四边形DEBF的周长为12 ,面积是4![]()
【解析】分析:(1)证明EF、BD互相平分,只要证DEBF是平行四边形;利用两组对边分别平行来证明.
(2)求四边形DEBF的周长,求出BE和DE即可.
详解:(1)∵四边形ABCD是平行四边形
∴CD∥AB,CD=AB,AD=BC
∵DE、BF分别是∠ADC和∠ABC的角平分线
∴∠ADE=∠CDE,∠CBF=∠ABF
∵CD∥AB,∴∠AED=∠CDE,∠CFB=∠ABF
∴∠AED=∠ADE,∠CFB=∠CBF
∴AE=AD,CF=CB,∴AE=CF,∴AB-AE=CD-CF 即BE=DF
∵DF∥BE,∴四边形DEBF是平行四边形
∵∠A=60°,AE=AD∴△ADE是等边三角形
∵AD=4,∴DE=AE=4,∵AE=2EB,∴BE=2
∴四边形DEBF的周长=2(BE+DE)=2(4+2)=12
过D点作DG⊥AB于点G,
在Rt△ADG中,AD=4,∠A=60°,
∴DG=ADcos∠A=4×![]() =
=![]()
∴四边形DEBF的面积=BE×DG=2×![]() =4
=4![]()

练习册系列答案
相关题目