Question

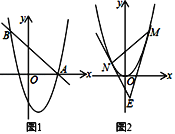
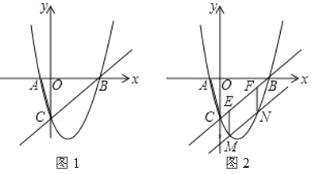
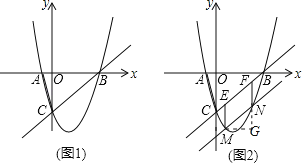
【题目】如图1，二次函数y＝ax2﹣3ax﹣4a的图象与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C(0，﹣3)．

（1）求二次函数的表达式及点A、点B的坐标；

（2）若点D在二次函数图象上，且，求点D的横坐标；

（3）将直线BC向下平移，与二次函数图象交于M，N两点（M在N左侧），如图2，过M作ME∥y轴，与直线BC交于点E，过N作NF∥y轴，与直线BC交于点F，当MN+ME的值最大时，求点M的坐标．

Answer 1

【答案】（1）y＝，A(﹣1，0)，B(4，0)；（2）2+2或2﹣2或2；（3）M(，﹣)

【解析】

（1）求出a，即可求解；
（2）求出直线BC的解析式，过点D作DH∥y轴，与直线BC交于点H，根据三角形面积的关系求解；
（3）过点M作MG∥x轴，交FN的延长线于点G，设M（m，m-3），N（n，n2-n-3），判断四边形MNFE是平行四边形，根据ME=NF，求出m+n=4，再确定ME+MN=-m2+3m+5-m=-（m-）2+ ，即可求M；

（1）y＝ax2﹣3ax﹣4a与y轴交于点C（0，﹣3），

∴a＝，

∴y＝，

与x轴交点A（﹣1，0），B（4，0）；

（2）设直线BC的解析式为y＝kx+b，

∴ ，
∴ ，

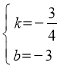∴y＝x﹣3；

过点D作DH∥y轴，与直线BC交于点H，

设H（x，x﹣3），D（x，x2﹣x﹣3），

∴DH＝|x2﹣3x|，

∵S△ABC＝，

∴S△DBC＝＝6，

∴S△DBC＝2×|x2﹣3x|＝6，

∴x＝2+2，x＝2﹣2，x＝2；

∴D点的横坐标为2+2，2﹣2，2；

（3）过点M作MG∥x轴，交FN的延长线于点G，

设M（m，m2﹣m﹣3），N（n，n2﹣n﹣3），

则E（m，m﹣3），F（n，n﹣3），

∴ME＝﹣m2+3m，NF＝﹣n2+3n，

∵EF∥MN，ME∥NF，

∴四边形MNFE是平行四边形，

∴ME＝NF，

∴﹣m2+3m＝﹣n2+3n，

∴m+n＝4，

∴MG＝n﹣m＝4﹣2m，

∴∠NMG＝∠OBC，

∴cos∠NMG＝cos∠OBC＝ ，

∵B（4，0），C（0，﹣3），

∴OB＝4，OC＝3，

在Rt△BOC中，BC＝5，

∴MN＝（n﹣m）＝（4﹣2m）＝5﹣m，

∴ME+MN＝﹣m2+3m+5﹣m＝﹣（m﹣）2+，

∵﹣＜0，

∴当m＝时，ME+MN有最大值，

∴M（，﹣）