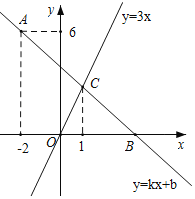ЬтФПФкШн
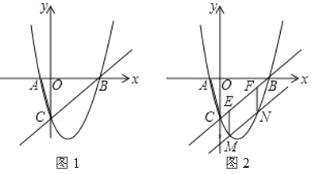
ЁОЬтФПЁП ШчЭМЃЌХзЮяЯпy=-x2+bx+cгыxжсНЛгкAЁЂBСНЕуЃЌНЛyжсе§АыжсгкCЕуЃЌDЮЊХзЮяЯпЕФЖЅЕуЃЌAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЎ
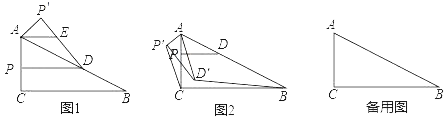
ЃЈ1ЃЉЧѓГіЖўДЮКЏЪ§ЕФБэДяЪНЃЎ
ЃЈ2ЃЉЕуPдкxжсЩЯЃЌЧвЁЯPCB=ЁЯCBDЃЌЧѓЕуPЕФзјБъЃЎ
ЃЈ3ЃЉдкxжсЩЯЗНХзЮяЯпЩЯЪЧЗёДцдквЛЕуQЃЌЪЙЕУвдQЃЌCЃЌBЃЌOЮЊЖЅЕуЕФЫФБпаЮБЛЖдНЧЯпЗжГЩУцЛ§ЯрЕШЕФСНВПЗжЃПШчЙћДцдкЃЌЧыжБНгаДГіЕуQЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=-x2+2x+3ЃЛЃЈ2ЃЉPЃЈ6ЃЌ0ЃЉЛђP![]() ЃЛЃЈ3ЃЉДцдкЃЌЕуQ
ЃЛЃЈ3ЃЉДцдкЃЌЕуQ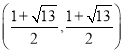 Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуAЁЂBзјБъДњШыНтЮіЪНЧѓГіbЁЂcЕФжЕМДПЩЕУЃЛ
ЃЈ2ЃЉЁЯPCB=ЁЯCBDгаСНжжЧщПіЃЌЂйPдкBЕФгвВрЪБЃЌбгГЄBDНЛyжсгкЕуHЃЌгЩЁЯOCB=ЁЯOBC=45ЁуЃЌПЩжЄУїЁЯHCB=ЁЯCBPЃЌДгЖјЁїPCBЁеЁїHBCЃЌгЩжБЯпBDМДПЩЧѓЕУЃКOH=OP=6ЃЌДгЖјЕУЕНPЕузјБъЃЛЂкPдкBЕФзѓВрЪБЃЌДЫЪБPCЁЮBDЃЌИљОнвЛДЮКЏЪ§НтЮіЪНМДПЩЧѓГіPЃЛ
ЃЈ3ЃЉЗжвдЯТСНжжЧщПіЗжБ№ЧѓНтЃЌЂйЕуQдкyжсгвВрЪБЃЌгЩOB=OCЃЌПЩЕУГіOQЪЧЁЯBOCЕФЦНЗжЯпЃЌСЊСЂЖўДЮКЏЪ§НтЮіЪНгыжБЯпOQЕФНтЮіЪНМДПЩЧѓНтЃЛЂкЕуQдкyжсзѓВрЪБЃЌПЩЕУетЬѕЖдНЧЯпжЛФмЪЧBQЃЌЙ§ЕуCзїxжсЕФЦНааЯпEFЃЌЙ§ЕуQЃЌBЗжБ№зїEFЕФДЙЯпЃЌДЙзуЗжБ№ЮЊFЃЌEЃЌбгГЄFQНЛxжсгкЕуGЃЌЩшЕуQЕФзјБъЮЊ(mЃЌn)ЃЌИљОнSЁїBOQ=SЁїCBQ=SЬнаЮFQBE-SЁїFCQ-SЁїBECПЩЕУГіЙигкmЃЌnЕФЙиЯЕЪНЃЌдйгыЖўДЮКЏЪ§ЕФНтЮіЪНСЊСЂМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉНЋЕуAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉДњШыy=-x2+bx+cЕУЃЌ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрЖўДЮКЏЪ§ЕФБэДяЪНЮЊy=-x2+2x+3ЃЛ
ЃЈ2ЃЉЂйЕБЕуPдкЕуBгвВрЪБЃЌбгГЄBDНЛyжсгкЕуHЃЌ

Ёпy=-x2+2x+3=-ЃЈx-1ЃЉ2+4ЃЌЁрЕуDЕФзјБъЮЊЃЈ1ЃЌ4ЃЉЃЌ
ЩшжБЯпBDЕФНтЮіЪНЮЊy=kx+bЃЌдђ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌМДжБЯпBDЕФНтЮіЪНЮЊy=-2x+6ЃЌ
ЃЌМДжБЯпBDЕФНтЮіЪНЮЊy=-2x+6ЃЌ
ЁрЕуHЕФзјБъЮЊЃЈ0ЃЌ6ЃЉЃЌ
ЁпOB=OC=3ЃЌЁрЁЯOBC=ЁЯOCB=45ЁуЃЌ
ЁрЁЯHCB=ЁЯCBP=135ЁуЃЌ
гжЁЯPCB=ЁЯCBDЃЌBC=BCЃЌ
ЁрЁїPCBЁеЁїHBCЃЌ
ЁрCH=PBЃЌ
ЁрOH=OB=6ЃЌ
ЙЪДЫЪБЕуPЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЃЛ
ЂкЕБЕуPЃЈPЁфЃЉдкЕуBзѓВрЪБЃЌ
жБЯпBDЕФБэДяЪНЮЊЃКy=-2x+6ЃЌ
ЁпЁЯPЁфCB=ЁЯCBDЃЌдђPЁфCЁЮBDЃЌ
дђжБЯпPЁфCЕФБэДяЪНЮЊЃКy=-2x+3ЃЌ
ЕБy=0ЃЌx=![]() ЃЌЙЪДЫЪБЕуPЁфЕФзјБъЮЊ
ЃЌЙЪДЫЪБЕуPЁфЕФзјБъЮЊ![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌЕуPЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЛђ![]() ЃЛ
ЃЛ
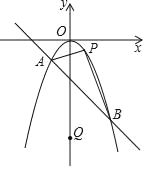
ЃЈ3ЃЉДцдкЃЎРэгЩШчЯТЃКЂйЕБЕуQдкyжсгвВрЪБЃЌвдQЃЌCЃЌBЃЌOЮЊЖЅЕуЕФЫФБпаЮБЛЖдНЧЯпЗжГЩУцЛ§ЯрЕШЕФСНВПЗжЃЌетЬѕЖдНЧЯпжЛФмЪЧOQЃЌSЁїCOQ=SЁїBOQЃЌШчЭМЃЌ
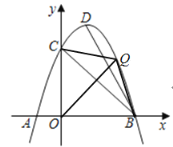
ЖјOB=OCЃЌЙЪOQЪЧЁЯBOCЕФЦНЗжЯпЃЌ
МДOQЕФКЏЪ§БэДяЪНЮЊЃКy=xЃЌ
НЋy=xгыy=-x2+2x+3СЊСЂЕУЃЌ
-x2+2x+3=xЃЌНтЕУx=![]() ЃЈЩсШЅИКжЕЃЉЃЌ
ЃЈЩсШЅИКжЕЃЉЃЌ
ЙЪДЫЪБЕуQЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЂкЕБЕуQдкyжсзѓВрЪБЃЌвдQЃЌCЃЌBЃЌOЮЊЖЅЕуЕФЫФБпаЮБЛЖдНЧЯпЗжГЩУцЛ§ЯрЕШЕФСНВПЗжЃЌетЬѕЖдНЧЯпжЛФмЪЧBQЃЌSЁїBOQ=SЁїCBQЃЌШчЭМЃЌЙ§ЕуCзїxжсЕФЦНааЯпEFЃЌЙ§ЕуQЃЌBЗжБ№зїEFЕФДЙЯпЃЌДЙзуЗжБ№ЮЊFЃЌEЃЌбгГЄFQНЛxжсгкЕуGЃЌдђQGЁЭxжсЃЌBE=CO=3=FGЃЌBO=CE=3ЃЌ
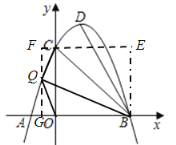
ЩшЕуQЕФзјБъЮЊ(mЃЌn)ЃЌдђQG=nЃЌFQ=3-nЃЌOG=FC=-mЃЌ
ЁрSЁїBOQ=![]() ЁС3ЁСnЃЌ
ЁС3ЁСnЃЌ
SЁїCBQ=SЬнаЮFQBE-SЁїFCQ-SЁїBEC=![]() ЁСЃЈ3-n+3ЃЉЁСЃЈ3-mЃЉ-
ЁСЃЈ3-n+3ЃЉЁСЃЈ3-mЃЉ-![]() ЁС(-m)ЁС(3-n)-
ЁС(-m)ЁС(3-n)-![]() ЁС3ЁС3=
ЁС3ЁС3=![]() (9-3m-3n)ЃЌ
(9-3m-3n)ЃЌ
Ёр![]() ЁС3ЁСn
ЁС3ЁСn![]() (9-3m-3n)ЃЌМДm+2n=3ЂйЃЌ
(9-3m-3n)ЃЌМДm+2n=3ЂйЃЌ
гжЕуQдкЖўДЮКЏЪ§ЭМЯѓЩЯЕУЃЌn=-m2+2m+3ЂкЃЌ
СЊСЂЂйЂкЕУЃЌ![]() ЃЌНтЕУ
ЃЌНтЕУ ЃЈ
ЃЈ![]() ЩсШЅЃЉЃЌ
ЩсШЅЃЉЃЌ
ЁрЕуQЕФзјБъЮЊЃЈ-![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
злЩЯЫљЪіЃЌЕуQЕФзјБъЮЊ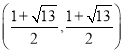 Лђ
Лђ![]() ЃЎ
ЃЎ