题目内容
【题目】小华同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.
(一)猜测探究
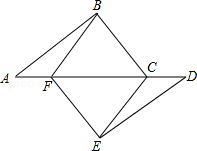
在△ABC中,AB=AC,M是平面内任意一点,将线段AM绕点A按顺时针方向旋转与∠BAC相等的角度,得到线段AN,连接NB.
(1)如图1,若M是线段BC上的任意一点,请直接写出∠NAB与∠MAC的数量关系是_______,NB与MC的数量关系是_______;
(2)如图2,点E是AB延长线上点,若M是∠CBE内部射线BD上任意一点,连接MC,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由。
(二)拓展应用
如图3,在△A1B1C1中,A1B1=8,∠A1B1C1=90°,∠C1=30°,P是B1C1上的任意点,连接A1P,将A1P绕点A1按顺时针方向旅转60°,得到线段A1Q,连接B1Q.求线段B1Q长度的最小值.

【答案】(一)(1)∠NAB=∠MAC,BN=MC;(2)成立,理由见解析;(二)QB1的最小值为4![]() -4
-4![]()
【解析】
(一)(1)由旋转知,AM=AN,∠BAC=∠NAM,进而得出∠MAC=∠NAB,判断出△CAM≌△BAN,即可得出结论;
(2)由旋转知,AM=AN,∠BAC=∠NAM,进而得出∠MAC=∠NAB,判断出△CAM≌△BAN,即可得出结论;
(二)如图3中,在A1 C1上截取A1N= A1 B1,连接PN,作NH⊥B1C1于H,作A1M⊥B1C1于M.理由全等三角形的性质证明B1Q=PN,推出当PN的值最小时,Q B1的值最小,求出HN的值即可解决问题.
解:(一)(1)结论:∠NAB=∠MAC,BN=MC.
理由:如图1中,
∵∠MAN=∠CAB,
∴∠NAB+∠BAM=∠BAM+∠MAC,
∴∠NAB=∠MAC,
∵AB=AC,AN=AM,
∴△NAB≌△MAC(SAS),
∴BN=CM.
故答案为:∠NAB=∠MAC,BN=CM,
(2)(1)中结论仍然成立,
理由:由旋转知,AM=AN,∠BAC=∠NAM,
∴∠BAC-∠BAM=∠NAM-∠BAM,
即:∠MAC=∠NAB,
∵AB=AC,
∴△CAM≌△BAN(SAS),
∴MC=NB;
(二)如图3中,在A1 C1上截取A1N= A1 B1,连接PN,作NH⊥B1 C1于H,作A1M⊥B1C1于M.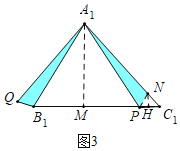
∵∠C1A B1=∠P A1Q,
∴∠Q A1 B1=∠P A1 N,
∵A1A= A1P,A1 B1=AN,
∴△Q A1 B1≌△P A1N(SAS),
∴B1Q=PN,
∴当PN的值最小时,Q B1的值最小,
在Rt△A1 B1M中,∵∠A1 B1M=60°,A1 B1=8,
∴A1M= A1 B1sin60°=4![]() ,
,
∵∠M A1 C1=∠B1 A1 C1-∠B1 A1M=75°-30°=45°,
∴A1 C1=4![]() ,
,
∴N C1= A1 C1- A1N=4![]() -8,
-8,
在Rt△NH C1,∵∠C1=45°,
∴NH=4![]() -4
-4![]() ,
,
根据垂线段最短可知,当点P与H重合时,PN的值最小,
∴Q B1的最小值为4![]() -4
-4![]()