题目内容
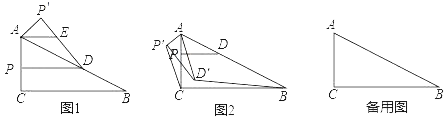
【题目】(感知)如图①,点C是AB中点,CD⊥AB,P是CD上任意一点,由三角形全等的判定方法“SAS”易证△PAC≌△PBC,得到线段垂直平分线的一条性质“线段垂直平分线上的点到线段两端的距离相等”

(探究)如图②,在平面直角坐标系中,直线y=-![]() x+1分别交x轴、y轴于点A和点B,点C是AB中点,CD⊥AB交OA于点D,连结BD,求BD的长
x+1分别交x轴、y轴于点A和点B,点C是AB中点,CD⊥AB交OA于点D,连结BD,求BD的长
(应用)如图③
(1)将线段AB绕点A顺时针旋转90°得到线段AB′,请在图③网格中画出线段AB;
(2)若存在一点P,使得PA=PB′,且∠APB′≠90°,当点P的横、纵坐标均为整数时,则AP长度的最小值为______.
【答案】探究:BD的长为![]() ;应用:(1)见解析;(2)5.
;应用:(1)见解析;(2)5.
【解析】
探究:根据直线解析式,求出点A、B坐标,得到BO、AO的长,设BD的长为a,根据勾股定理列方程可求出BD;
应用:(1)根据旋转的性质作图即可;
(2)根据题意可知P点坐标在AB’线段垂直平分线上,如图所示,点P’是垂直平分线上最近的格点,但是此时![]() ,不符合题意,根据网格特点可知垂直平分线上下一个格点位置,由网格特点和勾股定理可得符合题意的AP=5.
,不符合题意,根据网格特点可知垂直平分线上下一个格点位置,由网格特点和勾股定理可得符合题意的AP=5.
解:探究:
由题意得:
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
![]() ,
,![]() .
.
![]() ,
,![]() .
.
设BD的长为a.
∵点C是AB中点,![]() 交OA于点D,
交OA于点D,
![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() 的长为
的长为![]() .
.
应用:(1)如图,线段![]() 即为所求.
即为所求.
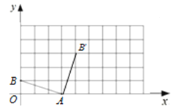
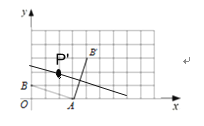
(2)根据题意可知P点坐标在AB’线段垂直平分线上,如图所示,点P’是垂直平分线上最近的格点,但是此时![]() ,不符合题意,根据网格特点可知垂直平分线上下一个格点位置,由网格特点和勾股定理可得符合题意的AP=5.
,不符合题意,根据网格特点可知垂直平分线上下一个格点位置,由网格特点和勾股定理可得符合题意的AP=5.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目