Question

【题目】已知抛物线：是由抛物线：平移得到的，并且的顶点为（1，－4）

（1）求的值；

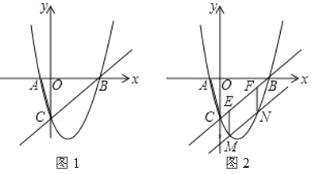
（2）如图1，抛物线C1与x轴正半轴交于点A，直线经过点A，交抛物线C1于另一点B．请你在线段AB上取点P，过点P作直线PQ∥y轴交抛物线C1于点Q，连接AQ．

①若AP＝AQ，求点P的坐标；

②若PA＝PQ，求点P的横坐标．

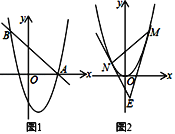
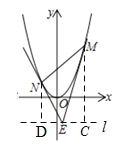
（3）如图2，△MNE的顶点M、N在抛物线C2上，点M在点N右边，两条直线ME、NE与抛物线C2均有唯一公共点，ME、NE均与y轴不平行．若△MNE的面积为16，设M、N两点的横坐标分别为m、n，求m与n的数量关系．

Answer 1

【答案】（1）；（2）①P点坐标为；②P点横坐标为﹣；（3）m﹣n＝4．

【解析】

（1）抛物线：是由抛物线：平移得到的，求出 ，

由抛物线的顶点为（1，－4），即可求出b、c的值；

（2）由直线经过点A，求出b的值，从而求出直线和抛物线的解析式，设P（t，﹣t+4），根据PQ∥y轴，推出Q（t，t2﹣2t﹣3），分两种情况：①当AP＝AQ时，②当AP＝PQ时，列出关于t的方程，即可求解；

（3）设经过的直线解析式为y＝k（x﹣m）+m2，直线ME与的方程联立得到方程组，由直线ME与有唯一公共点，得到k＝2m，直线ME的解析式为y＝2mx﹣m2，同理可求直线NE的解析式为y＝2nx﹣n2，求得E.过E作直线∥x轴，分别过M,N作的垂线，垂足为C，D，根据，列出关于m，n的方程，即可求解.

（1）∵抛物线：是由抛物线：平移得到的，

∴，

∵抛物线的顶点为（1，－4）

∴，，

∴，

∴

（2）y＝（x﹣1）2﹣4与x轴正半轴的交点A（3，0），

∵直线y＝﹣x+b经过点A，

∴b＝4，

∴y＝﹣x+4，

﹣x+4＝（x﹣1）2﹣4，

∴x＝3或x＝﹣，

∴B（﹣，），

设P（t，﹣t+4），且﹣＜t＜3，

∵PQ∥y轴，

∴Q（t，t2﹣2t﹣3），

①当AP＝AQ时，

|4﹣t|＝|t2﹣2t﹣3|，

则有﹣4+t＝t2﹣2t﹣3，

∴t＝，

∴P点坐标为

②当AP＝PQ时，

PQ＝t2+t+7，PA＝（3﹣t），

∴-t2+t+7＝（3﹣t），

∴t＝﹣；

∴P点横坐标为﹣

（3）设经过的直线解析式为y＝k（x﹣m）+m2，

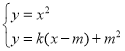，则有x2﹣kx+km﹣m2＝0，

∵直线ME与有唯一公共点,

∴△＝k2﹣4km+4m2＝（k﹣2m）2＝0，

∴k＝2m，直线ME的解析式为y＝2mx﹣m2，

同理可求直线NE的解析式为y＝2nx﹣n2，

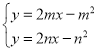
∴E，

如图，过E作直线∥x轴，分别过M,N作的垂线，垂足为C，D，

∴ [（n2﹣mn）+（m2﹣mn）]×（m﹣n）﹣（n2﹣mn）×（﹣n）﹣（m2﹣mn）×（m﹣）＝16，

∴（m﹣n）3＝64，

∴m﹣n＝4