Question

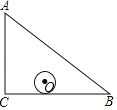
【题目】如图，在△ABC中，AC：BC：AB＝3：4：5，⊙O沿着△ABC的内部边缘滚动一圈，若⊙O的半径为1，且圆心O运动的路径长为18，则△ABC的周长为_____．

Answer 1

【答案】30

【解析】

如图，首先利用勾股定理判定△ABC是直角三角形，由题意得圆心O所能达到的区域是△DEG，且与△ABC三边相切，设切点分别为G、H、P、Q、M、N，连接DH、DG、EP、EQ、FM、FN，根据切线性质可得：AG＝AH，PC＝CQ，BN＝BM，DG、EP分别垂直于AC，EQ、FN分别垂直于BC，FM、DH分别垂直于AB，继而则有矩形DEPG、矩形EQNF、矩形DFMH，从而可知DE＝GP，EF＝QN，DF＝HM，DE∥GP，DF∥HM，EF∥QN，∠PEF＝90°,根据题意可知四边形CPEQ是边长为1的正方形，根据相似三角形的判定可得△DEF∽△ACB，根据相似三角形的性质可知：DE∶EF∶FD＝AC∶CB∶BA＝3∶4∶5，进而根据圆心O运动的路径长列出方程，求解算出DE、EF、FD的长，根据矩形的性质可得：GP、QN、MH的长，根据切线长定理可设：AG＝AH＝x，BN＝BM＝y，根据线段的和差表示出AC、BC、AB的长，进而根据AC∶CB∶BA＝3∶4∶5列出比例式，继而求出x、y的值，进而即可求解△ABC的周长．

∵AC∶CB∶BA＝3∶4∶5，

设AC＝3a，CB＝4a，BA＝5a（a＞0）

∴

∴△ABC是直角三角形，

设⊙O沿着△ABC的内部边缘滚动一圈，如图所示，

连接DE、EF、DF，

设切点分别为G、H、P、Q、M、N，

连接DH、DG、EP、EQ、FM、FN，

根据切线性质可得：

AG＝AH，PC＝CQ，BN＝BM

DG、EP分别垂直于AC，EQ、FN分别垂直于BC，FM、DH分别垂直于AB，

∴DG∥EP，EQ∥FN，FM∥DH,

∵⊙O的半径为1

∴DG＝DH＝PE＝QE＝FN＝FM＝1，

则有矩形DEPG、矩形EQNF、矩形DFMH，

∴DE＝GP，EF＝QN，DF＝HM，DE∥GP，DF∥HM，EF∥QN,∠PEF＝90°

又∵∠CPE＝∠CQE＝90°, PE＝QE＝1

∴四边形CPEQ是正方形，

∴PC＝PE＝EQ＝CQ＝1，

∵⊙O的半径为1，且圆心O运动的路径长为18，

∴DE+EF+DF＝18，

∵DE∥AC，DF∥AB，EF∥BC，

∴∠DEF＝∠ACB，∠DFE＝∠ABC，

∴△DEF∽△ABC，

∴DE：EF：DF＝AC：BC：AB＝3：4：5，

设DE＝3k（k＞0），则EF＝4k，DF＝5k，

∵DE+EF+DF＝18，

∴3k+4k+5k＝18，

解得k＝，

∴DE＝3k＝，EF＝4k＝6，DF＝5k＝，

根据切线长定理，

设AG＝AH＝x，BN＝BM＝y，

则AC＝AG+GP+CP＝x++1＝x+5．5，

BC＝CQ+QN+BN＝1+6+y＝y+7，

AB＝AH+HM+BM＝x++y＝x+y+7．5，

∵AC：BC：AB＝3：4：5，

∴（x+5．5）：（y+7）：（x+y+7．5）＝3：4：5，

解得x＝2，y＝3，

∴AC＝7．5，BC＝10，AB＝12．5，

∴AC+BC+AB＝30．

所以△ABC的周长为30．

故答案为30．