题目内容
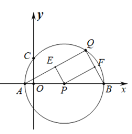
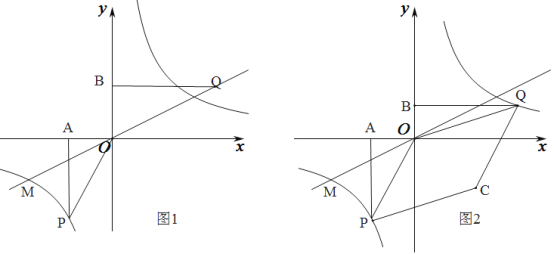
【题目】如图1，已知正比例函数和反比例函数的图象都经过点M（﹣2，﹣1），且P（﹣1，﹣2）为双曲线上的一点，Q为坐标平面上一动点，PA垂直于x轴，QB垂直于y轴，垂足分别是A、B．
（1）写出正比例函数和反比例函数的关系式；
（2）当点Q在直线MO上运动时，直线MO上是否存在这样的点Q，使得△OBQ与△OAP面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由；
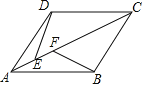
（3）如图2，当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的平行四边形OPCQ，求平行四边形OPCQ周长的最小值．
【答案】（1）y＝
x，
；（2）存在，Q1（2，1）和Q2（﹣2，﹣1）；（3）2
+4
【解析】
（1）正比例函数和反比例函数的图象都经过点M（-2，-1），待定系数法可求它们解析式；
（2）由点Q在y＝x上，设出Q点坐标，表示△OBQ，由反比例函数图象性质，可知△OAP面积为1，则根据面积相等可构造方程，问题可解；
（3）因为四边形OPCQ是平行四边形，所以OP=CQ，OQ=PC，而点P（-1，-2）是定点，所以OP的长也是定长，所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值．
解：（1）设正比例函数解析式为y＝kx，
将点M（﹣2，﹣1）坐标代入得k＝，所以正比例函数解析式为y＝x，
同样可得，反比例函数解析式为；
（2）当点Q在直线OM上运动时，
设点Q的坐标为Q（m，m），
于是S△OBQ＝OBBQ＝×m×m＝
m2，
而S△OAP＝|（﹣1）×（﹣2）|＝1，
所以有，m2＝1，解得m＝±2，
所以点Q的坐标为Q1（2，1）和Q2（﹣2，﹣1）；
（3）因为四边形OPCQ是平行四边形，所以OP＝CQ，OQ＝PC，
而点P（﹣1，﹣2）是定点，所以OP的长也是定长，
所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值，
因为点Q在第一象限中双曲线上，所以可设点Q的坐标为Q（n，
），
由勾股定理可得OQ2＝n2+
＝（n﹣）2+4，
所以当（n﹣）2＝0即n＝0时，OQ2有最小值4，
又因为OQ为正值，所以OQ与OQ2同时取得最小值，
所以OQ有最小值2，由勾股定理得OP＝，
所以平行四边形OPCQ周长的最小值是2（OP+OQ）＝2（+2）＝2+4．
（或因为反比例函数是关于y＝x对称，所以当Q在反比例函数时候，OQ最短的时候，就是反比例与y＝x的交点时候，联立方程组即可得到点Q坐标）
