题目内容
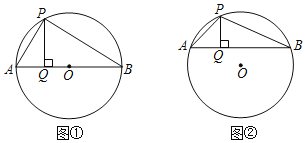
【题目】(1)如图①,AB为⊙O的直径,点P在⊙O上,过点P作PQ⊥AB,垂足为点Q.说明△APQ∽△ABP;
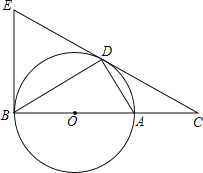
(2)如图②,⊙O的半径为7,点P在⊙O上,点Q在⊙O内,且PQ=4,过点Q作PQ的垂线交⊙O于点A、B.设PA=x,PB=y,求y与x的函数表达式.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据圆周角定理可证∠APB=90°,再根据相似三角形的判定方法:两角对应相等,两个三角形相似即可求证结论;
(2)连接PO,并延长PO交⊙O于点C,连接AC,根据圆周角定理可得∠PAC=90°,∠C=∠B,求得∠PAC=∠PQB,根据相似三角形的性质即可得到结论.
(1)如图①所示:
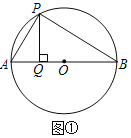
∵AB为⊙O的直径
∴∠APB=90°
又∵PQ⊥AB
∴∠AQP=90°
∴∠AQP=∠APB
又∵∠PAQ=∠BAP
∴△APQ∽△ABP.
(2)如图②,连接PO,并延长PO交⊙O于点C,连接AC.
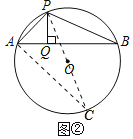
∵PC为⊙O的直径
∴∠PAC=90°
又∵PQ⊥AB
∴∠PQB=90°
∴∠PAC=∠PQB
又∵∠C=∠B(同弧所对的圆周角相等)
∴△PAC∽△PQB
∴![]()
又∵⊙O的半径为7,即PC=14,且PQ=4,PA=x,PB=y
∴![]()
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目