题目内容
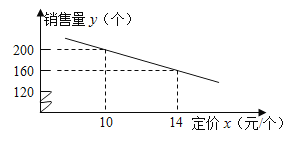
【题目】丹尼斯超市进了一批成本为 8 元/个的文具盒. 调查发现:这种文具盒每个星期的销售量y(个)与它的定价 x(元/个)的关系如图所示:
(1)求这种文具盒每个星期的销售量 y(个)与它的定价 x(元/个)之间的函数关系式(不必写出自变量 x的取值范围);
(2)每个文具盒的定价是多少元,超市每星期销售这种文具盒 (不考虑其他因素)可或得的利润为 1200 元?
(3)若该超市每星期销售这种文具盒的销售量小于 115 个, 且单件利润不低于 4 元(x 为整数),当每个文具盒定价多少 元时,超市每星期利润最高?最高利润是多少?
【答案】解:(1)![]() ;(2)当定价为18元或20元时,利润为1200元;(3)每个文具盒的定价是18元时,可获得每星期最高销售利润1200元.
;(2)当定价为18元或20元时,利润为1200元;(3)每个文具盒的定价是18元时,可获得每星期最高销售利润1200元.
【解析】
试题(1)由图可设函数关系式为![]() ,由图象过点(10,200)(14,160)即可根据待定系数法求解;
,由图象过点(10,200)(14,160)即可根据待定系数法求解;
(2)根据等量关系:总利润=单利润×总数量,即可列方程求解;
(3)先根据“每星期销售这种文具盒的销售量不少于115个,且单件利润不低于4元”求得x的取值范围,再根据等量关系:总利润=单利润×总数量,得到超市每星期的利润W与x的函数关系式,最后根据二次函数的性质求解即可.
(1)y=-10x+300;
(2)(x-8)·y=(x-8)(-10x+300)="1200"
解之得![]()
答:当定价为18元或20元时,利润为1200元;
(3)根据题意得:![]() ,
,![]()
得![]() ,且
,且![]() 为整数
为整数
设每星期所获利润为W元
则W=(x-8)·y=(x-8)(-10x+300)=-10(x2-38x+240)=-10(x-19) 2+1210
当x=18时,W有最大值, W最大=1200
每个文具盒的定价是18元时,可获得每星期最高销售利润1200元.