��Ŀ����
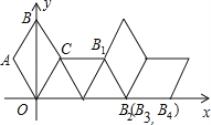
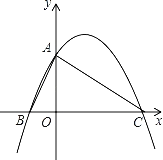
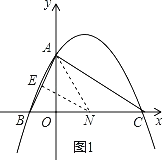
����Ŀ����ͼ�����κ���y��ax2+bx+c��a��0����ͼ����y�ύ�ڵ�A��0��4������x�Ḻ���ύ��B���������ύ�ڵ�C��8��0�����ҡ�BAC��90�㣮
��1����ö��κ�������ʽ��
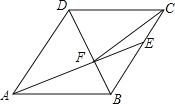
��2����N���߶�BC��һ���㣬��NE��AC����AB�ڵ�E������AN������ANE������ʱ�����N�����ꣻ
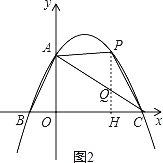
��3������PΪx���Ϸ����������ϵ�һ�����㣬����PA��PC�������á�PAC�����ΪS���ʣ��Ƿ����һ��S��ֵ��ʹ����Ӧ�ĵ�P����ֻ��2�������У�������S��ֵ�������ʱ��P�ĺ����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y����![]() x2+
x2+![]() x+4����2����3��0������3����S��16ʱ����Ӧ�ĵ�P����ֻ������
x+4����2����3��0������3����S��16ʱ����Ӧ�ĵ�P����ֻ������
��������
��1��֤��![]() �������B���꣬���ô���ϵ��������������κ�������ʽ��
�������B���꣬���ô���ϵ��������������κ�������ʽ��
��2����N��n��0������BN��n+2��BC��10��֤����BNE�ס�BAC���õ�S��BEN��![]() ��n+2��2�������S��BAN��2n+4�����ø�����
��n+2��2�������S��BAN��2n+4�����ø�����![]() �����ݶ��κ������ʼ�����⣻
�����ݶ��κ������ʼ�����⣻
��3����P![]() ���ֱ������0��m��8�ͩ�2��m��0ʱS��m������ϵʽ���������һ��S��ֵ��ʹ����Ӧ�ĵ�P����ֻ��2�����õ���S��16ʱ��m��4��m��
���ֱ������0��m��8�ͩ�2��m��0ʱS��m������ϵʽ���������һ��S��ֵ��ʹ����Ӧ�ĵ�P����ֻ��2�����õ���S��16ʱ��m��4��m��![]() ������������ý⣮
������������ý⣮
�⣺��1���ߡ�BAC��90�㣬��AOC=![]() ��90�㣬
��90�㣬
��![]()
![]()
![]()
![]()
��OA2��OBOC��
������֪��OA��4��OC��8��
��42��OB8��
��OB��2��
��B����2��0����
��A��B��C����������뼴�ã�
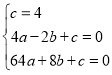 ��
��
��ã�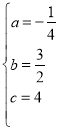 ��
��
�������߽���ʽΪ��y����![]() x2+
x2+![]() x+4��
x+4��
��2����N��n��0������BN��n+2��BC��10��
��NE��AC��
���BNE�ס�BAC��
��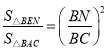 ��
��
��S��AC��![]() ��10��4��20��
��10��4��20��
��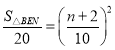 ��
��
S��BEN��![]() ��n+2��2��
��n+2��2��
��S��BAN��![]() ����n+2����4��2n+4��
����n+2����4��2n+4��
��![]() ��
��
��![]() ��
��
�൱n��3ʱ�����ֵS��ANE��5��
��ʱN������Ϊ����3��0����
��3����ֱ��AC��Ӧ�ĺ�������ʽΪ��y��kx+b��
��![]() ��
��
��ã�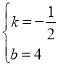 ��
��
��ֱ��AC��Ӧ�ĺ�������ʽΪ![]() ��
��
��ͼ����P��PH��OC������ΪH����ֱ��AC�ڵ�Q��
��P![]() ����Q
����Q![]() ��
��
�ٵ�0��m��8ʱ��
PQ![]() ��
��
S��S��APQ+S��CPQ��![]() ��8��
��8��![]() ������m��4��2+16��
������m��4��2+16��
��0��S��16��
�ڵ���2��m��0ʱ��
PQ����![]() ������
������![]() ����
����![]() ��
��
S��S��CPQ��S��APQ��![]() ��8����
��8����![]() ������m��4��2��16��
������m��4��2��16��
��0��S��20��
�൱0��S��16ʱ��0��m��8����m����ֵ����2��m��0��m��һ��ֵ����ʱ��������
��16��S��20ʱ����2��m��0��mֻ��һ��ֵ��
��S��16ʱ��m��4��m��![]() ��������
��������
�ʵ�S��16ʱ����Ӧ�ĵ�P����ֻ��������

 ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д�