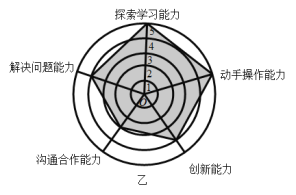
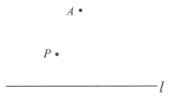ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌбгГЄ
ЃЌбгГЄ![]() ЪЙ
ЪЙ![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ШЦЕуCЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮ
ШЦЕуCЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮ![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЎ
ЃЎ
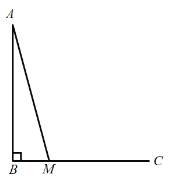
ЃЈ1ЃЉвРОнЬтвтВЙШЋЭМаЮЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФЖШЪ§ЪЧ__________ЃЛ
ЕФЖШЪ§ЪЧ__________ЃЛ
ЃЈ3ЃЉаЁДЯЭЈЙ§ЛЭМЁЂВтСПЗЂЯжЃЌЕБ![]() ЪЧвЛЖЈЖШЪ§ЪБЃЌ
ЪЧвЛЖЈЖШЪ§ЪБЃЌ![]() ЃЎ
ЃЎ
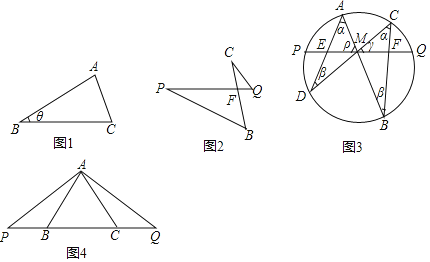
аЁДЯАбетИіВТЯыКЭЭЌбЇУЧНјааНЛСїЃЌЭЈЙ§ЬжТлЃЌаЮГЩСЫжЄУїИУВТЯыЕФМИжжЯыЗЈЃК
ЯыЗЈ1ЃКЭЈЙ§ЙлВьЭМаЮПЩвдЗЂЯжЃЌШчЙћАбЬнаЮ![]() ВЙШЋГЩЮЊе§ЗНаЮ
ВЙШЋГЩЮЊе§ЗНаЮ![]() ЃЌОЭвзжЄ
ЃЌОЭвзжЄ![]() ЃЌвђДЫвзЕУЕБ
ЃЌвђДЫвзЕУЕБ![]() ЪЧЬиЪтжЕЪБЃЌЮЪЬтЕУжЄЃЛ
ЪЧЬиЪтжЕЪБЃЌЮЪЬтЕУжЄЃЛ
ЯыЗЈ2ЃКвЊжЄ![]() ЃЌЭЈЙ§ЕкЃЈ2ЃЉЮЪЃЌПЩжЊжЛашвЊжЄУї
ЃЌЭЈЙ§ЕкЃЈ2ЃЉЮЪЃЌПЩжЊжЛашвЊжЄУї![]() ЪЧЕШБпШ§НЧаЮЃЌЭЈЙ§ЙЙдьЦНааЫФБпаЮ
ЪЧЕШБпШ§НЧаЮЃЌЭЈЙ§ЙЙдьЦНааЫФБпаЮ![]() ЃЌвзжЄ
ЃЌвзжЄ![]() ЃЌЭЈЙ§
ЃЌЭЈЙ§![]() ЃЌвзжЄ
ЃЌвзжЄ![]() ЃЌДгЖјНтОіЮЪЬтЃЛ
ЃЌДгЖјНтОіЮЪЬтЃЛ
ЯыЗЈ3ЃКЭЈЙ§![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЌвзжЄ
ЃЌвзжЄ![]() ЃЌвзЕУ
ЃЌвзЕУ![]() ЪЧЕШбќШ§НЧаЮЃЌвђДЫЕБ
ЪЧЕШбќШ§НЧаЮЃЌвђДЫЕБ![]() ЪЧЬиЪтжЕЪБЃЌЮЪЬтЕУжЄЃЎ
ЪЧЬиЪтжЕЪБЃЌЮЪЬтЕУжЄЃЎ
ЧыФуВЮПМЩЯУцЕФЯыЗЈЃЌАяжњаЁДЯжЄУїЕБ![]() ЪЧвЛЖЈЖШЪ§ЪБЃЌ
ЪЧвЛЖЈЖШЪ§ЪБЃЌ![]() ЃЎЃЈвЛжжЗНЗЈМДПЩЃЉ
ЃЎЃЈвЛжжЗНЗЈМДПЩЃЉ
ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉ60ЁуЃЛЃЈ3ЃЉЕБ![]() ЪБНсТлГЩСЂЃЌЯъМћНтЮі
ЪБНсТлГЩСЂЃЌЯъМћНтЮі
ЁОНтЮіЁП
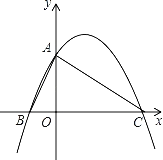
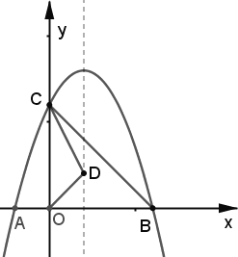
(1)ИљОнЬтвтВЙШЋЭМаЮМДПЩЕУЕНД№АИЃЛ
(2)ЯШЫуГі![]() ЃЌдйИљОна§зЊЕФаджЪЕУЕН
ЃЌдйИљОна§зЊЕФаджЪЕУЕН![]() ЃЌдйЯрМѕМДПЩЕУЕНД№АИЃЛ
ЃЌдйЯрМѕМДПЩЕУЕНД№АИЃЛ
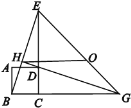
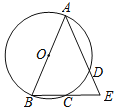
(3) жЄУїЯыЗЈвЛЃЌЙ§Aзї![]() гкEЃЌЯШжЄУїЫФБпаЮ
гкEЃЌЯШжЄУїЫФБпаЮ![]() ЪЧе§ЗНаЮЃЌЕУЕН
ЪЧе§ЗНаЮЃЌЕУЕН![]() ЃЌдйжЄУї
ЃЌдйжЄУї![]() МДПЩЕУЕНД№АИЃЛ
МДПЩЕУЕНД№АИЃЛ
НтЃКЃЈ1ЃЉВЙШЋЭМаЮ
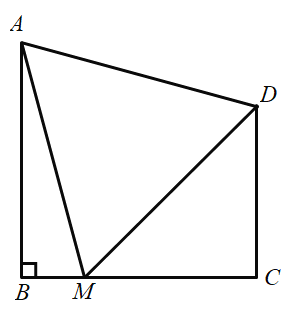
ЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ
![]() ,
,
ЁпЯпЖЮ![]() ШЦЕуCЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮ
ШЦЕуCЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮ![]() ЃЌ
ЃЌ
Ёр![]() ,
,
Ёр![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК60Ёу ЃЛ
ЃЈ3ЃЉЕБ![]() ЪБНсТлГЩСЂЃЎ
ЪБНсТлГЩСЂЃЎ
жЄУїЃКЯыЗЈвЛЃК
Й§Aзї![]() гкEЃЎ
гкEЃЎ
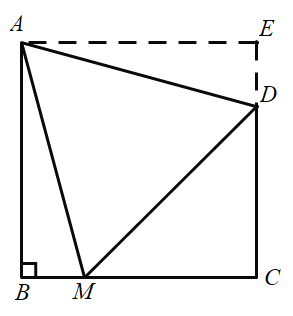
Ёп![]()
![]()
ЁрЫФБпаЮ![]() ЪЧе§ЗНаЮ ЃЌ
ЪЧе§ЗНаЮ ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ
Ёр![]() ЪЧЕШБпШ§НЧаЮ
ЪЧЕШБпШ§НЧаЮ
Ёр![]() ЃЛ
ЃЛ