题目内容
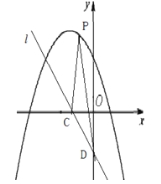
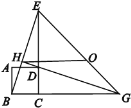
【题目】在平面直角坐标系中,正方形![]() .... 按如图的方式放置.点
.... 按如图的方式放置.点![]()
![]() 和点
和点![]() 分别落在直线
分别落在直线![]() 和
和![]() 轴上.抛物线
轴上.抛物线![]() 过点
过点![]() ,且顶点在直线
,且顶点在直线![]() 上,抛物线
上,抛物线![]() 过点
过点![]() ,且顶点在直线
,且顶点在直线![]() 上,...按此规律,抛物线
上,...按此规律,抛物线![]() ,过点
,过点![]() , 且顶点也在直线
, 且顶点也在直线![]() 上,其中抛物线
上,其中抛物线![]() 交正方形
交正方形![]() 的边
的边![]() 于点
于点![]() ,抛物线
,抛物线![]() 交正方形
交正方形![]() 的边
的边![]() 于点
于点![]() (其中
(其中![]() 且
且![]() 为正整数) .
为正整数) .

(1)直接写出下列点的坐标:![]() ,
,![]() ;
;
(2)写出抛物线![]() 的解析式,并写出抛物线
的解析式,并写出抛物线![]() 的解析式求解过程,再猜想抛物线
的解析式求解过程,再猜想抛物线![]() 的顶点坐标;
的顶点坐标;
(3)设![]() ,试判断
,试判断![]() 与
与![]() 的数量关系并说明理由.
的数量关系并说明理由.
【答案】(1)![]() ;(2)抛物线
;(2)抛物线![]() 的解析式为:
的解析式为:![]() ,抛物线
,抛物线![]() 的解析式为
的解析式为![]() ,抛物线
,抛物线![]() 的解析式过程见解析;抛物线
的解析式过程见解析;抛物线![]() 的顶点坐标为
的顶点坐标为![]() ;(3)
;(3)![]() 与
与![]() 的数量关系为
的数量关系为![]() ,理由见解析.
,理由见解析.
【解析】
(1)先求出A1坐标,根据正方形性质,求出B1坐标,进而求出A2坐标,最后求出B2坐标;
(2)根据A2点B2的坐标求出抛物线![]() 的对称轴,根据
的对称轴,根据![]() 的顶点在
的顶点在![]() 上求出顶点坐标,进而利用顶点式求出
上求出顶点坐标,进而利用顶点式求出![]() 解析式;根据A3B3的坐标求出抛物线
解析式;根据A3B3的坐标求出抛物线![]() 的对称轴,根据
的对称轴,根据![]() 的顶点在
的顶点在![]() 上求出顶点坐标,进而利用顶点式求出
上求出顶点坐标,进而利用顶点式求出![]() 解析式;写出
解析式;写出![]() 三条抛物线的顶点坐标,找出规律,写出
三条抛物线的顶点坐标,找出规律,写出![]() 的顶点坐标;
的顶点坐标;
(3)根据(2)求出D1,D2坐标,进而求出![]() ,
,![]() ,
,![]() ,
,![]() 长, 最后求出
长, 最后求出![]() ,比较即可 .
,比较即可 .
解:(1)把x=0代入![]() 得y=-1,∴点A1坐标为(0,-1) ;
得y=-1,∴点A1坐标为(0,-1) ;
∵四边形![]() 是正方形
是正方形
∴A1 B1=1,∴点B1坐标为(0,-1) ;
把x=1代入![]() 得y=-2,∴点A2坐标为(1,-2) ;
得y=-2,∴点A2坐标为(1,-2) ;
∵四边形![]() 是正方形
是正方形
∴A2 B2=2,∴点B2坐标为(3,-2) ;
∴![]()
(2)解:由(1)得点A2坐标为(1,-2),点B2坐标为(3,-2),
![]() 抛物线
抛物线![]() 的对称轴为直线
的对称轴为直线![]()
把![]() 代入
代入![]() 得
得![]() ,
,
![]() 抛物线
抛物线![]() 的顶点为
的顶点为![]()
设抛物线![]() 的解析式为:
的解析式为: ![]()
![]() 抛物线
抛物线![]() 过点
过点![]()
![]() 当
当![]() 时,
时,![]()
![]()
解得![]()
![]() 抛物线
抛物线![]() 的解析式为:
的解析式为:![]()
把![]() 代入
代入![]() 得
得![]() ,∴点A3坐标为(3,-4)
,∴点A3坐标为(3,-4)
∵四边形![]() 是正方形
是正方形
∴A3 B3=4,∴点B3坐标为(7,-4) ;
∴![]() 抛物线
抛物线![]() 的对称轴为直线
的对称轴为直线![]()
把![]() 代入
代入![]() 得
得![]() ,
,
![]() 抛物线
抛物线![]() 的顶点为
的顶点为![]()
设抛物线![]() 的解析式为:
的解析式为: ![]() ,
,
![]() 抛物线
抛物线![]() 过点
过点![]()
![]()
解得![]()
![]() 抛物线
抛物线![]() 的解析式为:
的解析式为:![]() ,
,
根据抛物线![]() 的顶点为
的顶点为![]()
抛物线![]() 的顶点为
的顶点为![]() ,
,
抛物线![]() 的顶点为
的顶点为![]()
得抛物线![]() 的顶点坐标为
的顶点坐标为![]()
(3)![]() 与
与![]() 的数量关系为
的数量关系为![]()
理由如下;由(2)得抛物线![]() 的解析式为
的解析式为![]()
当![]() 时,
时,![]()
解得![]() (舍去)
(舍去)
![]()
即![]()
由(2)得抛物线![]() 的解析式为
的解析式为
当![]() 时,
时,![]()
解得![]() (舍去)
(舍去)
![]()
![]()
![]()
即![]()
![]() .
.

【题目】自从开展“创建全国文明城区“工作以来,门头沟区便掀起了“门头沟热心人“志愿服务的热潮,区教委也号召各校学生积极参与到志愿服务当中.为了解甲、乙两所学校学生一周志愿服务情况,从这两所学校中各随机抽取40名学生,分别对他们一周的志愿服务时长(单位:分钟)数据进行收集、整理、描述和分析.下面给出了部分信息:
a.甲校40名学生一周的志愿服务时长的扇形统计图如图(数据分成6组:![]() ):
):
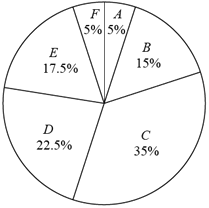
A:![]() B:
B:![]()
C:![]() D:
D:![]()
E:![]() F:
F:![]()
b.甲校40名学生一周志愿服务时长在![]() 这一组的是:
这一组的是:
60 60 62 63 65 68 70 72 73 75 75 76 80 80
c.甲、乙两校各抽取的40名学生一周志愿服务时长的平均数、中位数、众数如下:
学校 | 平均数 | 中位数 | 众数 |
甲校 | 75 |
| 90 |
乙校 | 75 | 76 | 85 |
根据以上信息,回答下列问题:
(1)![]() _____________;
_____________;
(2)根据上面的统计结果,你认为____①_____所学校学生志愿服务工作做得好(填“甲“或“乙“),理由______②________________________________________________________;
(3)甲校要求学生一周志愿服务的时长不少于60分钟,如果甲校共有学生800人,请估计甲校学生中一周志愿服务时长符合要求的有_______人.