Question

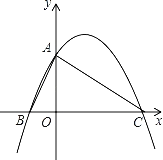
【题目】在平面直角坐标系中，已知抛物线与x轴交于点，且．抛物线与y轴交于点C，将点C向上移动1个单位得到点D．

（1）求抛物线对称轴；

（2）求点D纵坐标（用含有a的代数式表示）；

（3）已知点，若抛物线与线段只有一个公共点，求a的取值范围．

Answer 1

【答案】（1）对称轴；（2）；（3）当或时，抛物线与线段只有一个交点．

【解析】

（1）直接根据二次函数的对称轴计算即可；

（2）根据，对称轴可得， ，把代入得，则有，可得C点坐标为，再根据平移，可得D纵坐标；

（3）分两种情况：当和当对抛物线的图像进行讨论即可．

（1）抛物线的对称轴为：

（2），对称轴

可得，

把代入得：

∴

∴C点坐标为，

，

（3）如图示，

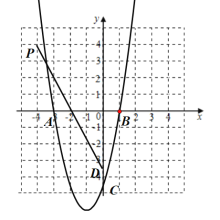
①当时

将点代入抛物线得：

，

结合函数图象，可得当时，抛物线与线段只有一个交点；

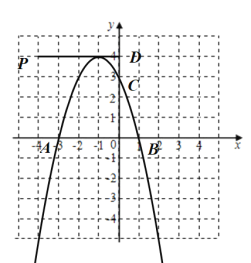
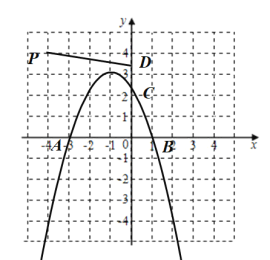
②如下图示，当时，

抛物线的顶点为，

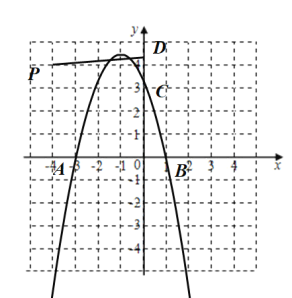
结合函数图象，可得当时，抛物线与线段只有一个交点，

∴ ，

综上所述，当或时，抛物线与线段只有一个交点．