Question

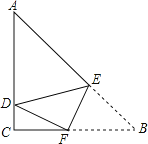
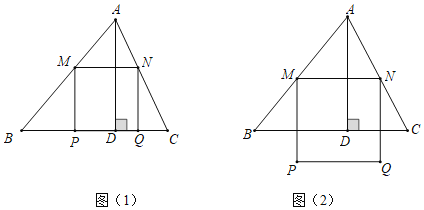
【题目】如图在锐角△ABC中，BC＝6，高AD＝4，两动点M、N分别在AB、AC上滑动(不包含端点)，且MN∥BC，以MN为边长向下作正方形MPQN，设MN＝x，正方形MPQN与△ABC公共部分的面积为y．

(1)如图(1)，当正方形MPQN的边P恰好落在BC边上时，求x的值；

(2)如图(2)，当PQ落△ABC外部时，求出y与x的函数关系式(写出x的取值范围)并求出x为何值时y最大，最大是多少？

Answer 1

【答案】(1)x=2.4；(2)如图(2)当x＝3时，y有最大值，最大值是6．

【解析】

（1）利用相似三角形的判定和性质列比例式求解；（2）利用相似三角形的判定和性质列比例式求正方形MPQN与△ABC公共部分的长和宽，从而列出函数关系式并求最值.

(1)当PQ恰好落在边BC上时，

∵MN∥BC，

∴△AMN∽△ABC

∴，

∵以MN为边长向下作正方形MPQN

∴GD=MN=4

即，

∴x＝ ．

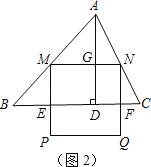
(2)设BC分别交MP，NQ于E，F，则四边形MEFN为矩形．

设ME＝NF＝h，AD交MN于G(如图2)GD＝NF＝h，AG＝4﹣h．

∵MN∥BC，

∴△AMN∽△ABC．

∴，即，，

∴h＝x+4．

∴y＝MNNF＝x(x+4)＝x2+4x(2.4＜x＜6)，

配方得：y＝(x﹣3)2+6．

∴当x＝3时，y有最大值，最大值是6．