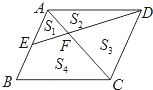
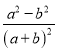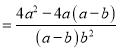题目内容
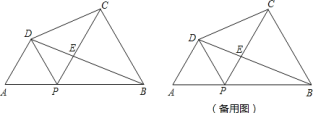
【题目】如图,已知线段![]() ,
,![]() 是线段
是线段![]() 上任意一点(不与点
上任意一点(不与点![]() 、
、![]() 重合),分别以
重合),分别以![]() 、
、![]() 为边,在
为边,在![]() 的同侧作等边
的同侧作等边![]() 和
和![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
![]() 当
当![]() 时,试求
时,试求![]() 的正切值;
的正切值;
![]() 若线段
若线段![]() 是线段
是线段![]() 和
和![]() 的比例中项,试求这时
的比例中项,试求这时![]() 的值;
的值;
![]() 记四边形
记四边形![]() 的面积为
的面积为![]() ,当
,当![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 与
与![]() 是否成正比例,若成正比例,试求出比例系数;若不成正比例,试说明理由.
是否成正比例,若成正比例,试求出比例系数;若不成正比例,试说明理由.
【答案】![]() ;
;![]() ,
,![]()
![]() 与
与![]() 成正比例,比例系数为
成正比例,比例系数为![]() .
.
【解析】
(1) 根据等边三角形的性质得出PC=BC,∠CPD=![]() , PD//BC, 进而得出∠DBC的
, PD//BC, 进而得出∠DBC的
正切值等于![]() ,即可得出答案;
,即可得出答案;
(2) 利用线段CD是线段DE和DB的比例中项得出△DCE∽△BCD, 再利用相似三角形的性质得出即可;
(3)由AD//PC,PD//BC,得出
![]() ,
,![]()
进而得出
![]() ,以及
,以及![]()
即可得出比例系数.
![]() ∵等边
∵等边![]() 和
和![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 由已知,
由已知,![]() ,
,
即![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即点
,即点![]() 是线段
是线段![]() 的黄金分割点.
的黄金分割点.
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,![]() 设
设![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
作![]() ,
,
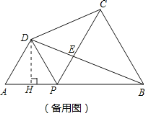
则![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 与
与![]() 成正比例,比例系数为
成正比例,比例系数为![]() .
.

练习册系列答案
相关题目