题目内容
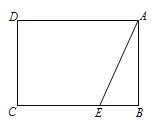
【题目】已知矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点,
上一点,![]() ,连接
,连接![]() .
.
(1)沿![]() 翻折
翻折![]() 使点
使点![]() 落在点
落在点![]() 处,
处,
①连接![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
②连接![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
(2)![]() 绕点
绕点![]() 顺时针旋转得
顺时针旋转得![]() ,点
,点![]() 落在边
落在边![]() 上时旋转停止. 若点
上时旋转停止. 若点![]() 落在矩形对角线
落在矩形对角线![]() 上,且点
上,且点![]() 到
到![]() 的距离小于
的距离小于![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)①2;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①由CF∥AE可得内错角和同位角相等,由翻折有对应角相等,等量代换后出现等腰三角形,即可求出m值;②过点F作GH⊥AD于点G,交BC于点H,根据相似三角形的对应边成比例求翻折后AG和FG的长度,再根据勾股定理列出DF2与m的二次函数关系根据抛物线的性质求出自变量m的范围;
(2)过点B1作MN⊥AD于点M,交BC于点N,由△AMB1∽△CBA得出对应边成比例列出比例式,用含m的式子表示B1M,根据题意求出m的范围,再根据当E1落在AD上时,此时m最大,根据△AB1E1∽△ABE求出m的最大值,从而确定m的取值范围.
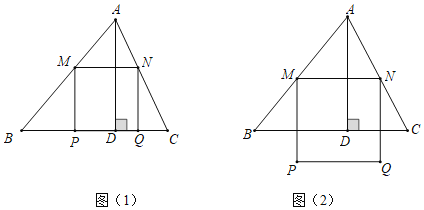
解:(1)①如图,
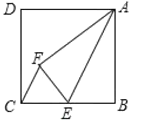
∵CF∥AE,
∴∠FCE=∠AEB, ∠CFE=∠AEF,
∵△ABE翻折得到△AFE,
∴EF=EB=1,∠AEF=∠AEB,
∴∠ECF=∠EFC,
∴CE=EF=1,
∴m=BC=BE+CE=2.
②如图,过点F作GH⊥AD于点G,交BC于点H,
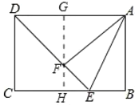
∴∠AGH=∠GHB=∠B=90°,
∴四边形AGHB是矩形,
∴AG=BH,GH=AB=2,
由折叠可知,∠B=∠AFE=90°,BE=FE=1,AF=AB=2,
∵∠GAF+∠AFG=90°, ∠AFG+∠EFH=90°,
∴∠GAF=∠EFH,
∴△AGF∽△HFE,
∴![]() ,
,
设AG=a,GF=b,则有,
![]() ,
,
解得:a=![]() ,b=
,b=![]() ,
,
∵AD=BC=m,
∴DG=![]() =
=![]() ,
,
∴DF2=DG2+FG2=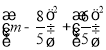 =
= 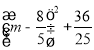 ,
,
∴DF2与m成二次函数关系,且抛物线开口向上,当m=![]() 时,DF2有最小值为
时,DF2有最小值为![]() ,
,
∵![]() ,
,
∴![]() ,
,
当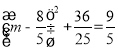 时,
时,
解得m1=1,m2=![]() ,
,
∴由二次函数图象的性质可得,![]() .
.
(2)如图,过点B1作MN⊥AD于点M,交BC于点N,
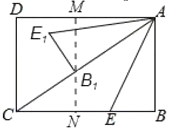
∴∠AMB1=∠B=90°,
∵AD∥BC,
∴∠MAB1=∠ACB,
∴△AMB1∽△CBA,
∴![]() ,
,
由翻折可知AB1=AB=2,
∴![]() ,
,
∴B1M=![]() ,
,
∵点B1到![]() 的距离小于
的距离小于![]() ,
,
∴![]() <
<![]() ,解得m>
,解得m>![]() .
.
如图,当点E1落在边AD上时,且点B1在AC上时,m最大,
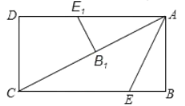
∵∠AB1E1=∠ABC, ∠E1AB=∠ACB,
∴△AB1E1∽△ABE,
∴![]() ,即
,即![]() ,
,
∴m=4,
∴m的取值范围是![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案