题目内容
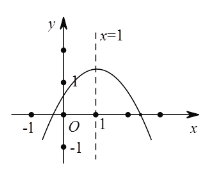
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
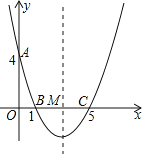
【答案】(1)y=![]() x2﹣
x2﹣![]() x+4;(2)P(3,
x+4;(2)P(3,![]() );(3)N(
);(3)N(![]() ,﹣3).
,﹣3).
【解析】
(1)抛物线经过点A(0,4),B(1,0),C(5,0),可利用两点式法设抛物线的解析式为y=a(x1)(x5),代入A(0,4)即可求得函数的解析式;
(2)点A关于对称轴的对称点A′的坐标为(6,4),连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小,求出直线BA′的解析式,即可得出点P的坐标;
(3)设N点的横坐标为t,此时点N(t,![]() t2﹣
t2﹣![]() t+4)(0<t<5),再求得直线AC的解析式,即可求得NG的长与△ACN的面积,由二次函数最大值的问题即可求得答案.
t+4)(0<t<5),再求得直线AC的解析式,即可求得NG的长与△ACN的面积,由二次函数最大值的问题即可求得答案.
解:(1)根据已知条件可设抛物线的解析式为y=a(x﹣1)(x﹣5),
把点A(0,4)代入上式得:a=![]() ,
,
∴y=![]() (x﹣1)(x﹣5)=
(x﹣1)(x﹣5)=![]() x2﹣
x2﹣![]() x+4;=
x+4;=![]() (x﹣3)2﹣
(x﹣3)2﹣![]() ,
,
(2)∵点A(0,4),抛物线的对称轴是x=3,
∴点A关于对称轴的对称点A′的坐标为(6,4),
如图1,连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小.
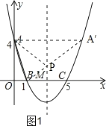
设直线BA′的解析式为y=kx+b,
把A′(6,4),B(1,0)代入得![]() ,解得
,解得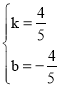 ,
,
∴y=![]() x﹣
x﹣![]() ,
,
∵点P的横坐标为3,
∴y=![]() ×3﹣
×3﹣![]() =
=![]() ,
,
∴P(3,![]() );
);
(3)设N点的横坐标为t,此时点N(t,![]() t2﹣
t2﹣![]() t+4)(0<t<5),
t+4)(0<t<5),
如图2,过点N作NG∥y轴交AC于G,作AD⊥NG于D,
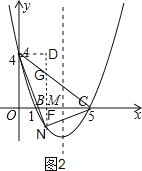
由点A(0,4)和点C(5,0)可求出直线AC的解析式为:y=﹣![]() x+4,
x+4,
把x=t代入得:y=﹣![]() t+4,则G(t,﹣
t+4,则G(t,﹣![]() t+4),
t+4),
此时:NG=﹣![]() t+4﹣(
t+4﹣(![]() t2﹣
t2﹣![]() t+4)=﹣
t+4)=﹣![]() t2+4t,
t2+4t,
∵AD+CF=CO=5,
∴S△ACN=S△ANG+S△CGN=![]() AM×NG+
AM×NG+![]() NG×CF=
NG×CF=![]() NGOC=
NGOC=![]() ×(﹣
×(﹣![]() t2+4t)×5=﹣2t2+10t=﹣2(t﹣
t2+4t)×5=﹣2t2+10t=﹣2(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,△CAN面积的最大值为
时,△CAN面积的最大值为![]() ,
,
由t=![]() ,得:y=
,得:y=![]() t2﹣
t2﹣![]() t+4=﹣3,
t+4=﹣3,
∴N(![]() ,﹣3).
,﹣3).

 一本好题口算题卡系列答案
一本好题口算题卡系列答案