题目内容
如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):

(1)利用网格确定该圆弧所在圆的圆心D点的位置,并写出D点的坐标为 ;
(2)连接AD、CD,则⊙D的半径为 ,∠ADC的度数为 ;
(3)若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.

(1)利用网格确定该圆弧所在圆的圆心D点的位置,并写出D点的坐标为 ;
(2)连接AD、CD,则⊙D的半径为 ,∠ADC的度数为 ;
(3)若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.
(1)D点的坐标为(2,0);
(2)连接AD、CD,则⊙D的半径为 ,∠ADC的度数为90°;
,∠ADC的度数为90°;
(3)若扇形DAC是一个圆锥的侧面展开图,则该圆锥底面半径为 .
.
(2)连接AD、CD,则⊙D的半径为
 ,∠ADC的度数为90°;
,∠ADC的度数为90°;(3)若扇形DAC是一个圆锥的侧面展开图,则该圆锥底面半径为
 .
.试题分析:(1)由垂径定理画出图形,再根据图形即可得出点的坐标;
(2)根据勾股定理即可求出⊙D的半径;利用勾股定理逆定理;
(3)根据坐标推出OA=DF,OD=CF,证△AOD≌△DFC 即可得△ADC是直角三角形,∠ADC=90°;
(4)根据圆的周长和弧长公式求出即可.
试题解析:(1)如图所示:

D点的坐标为(2,0);
(2)由勾股定理得:
 ,故⊙D的半径为:
,故⊙D的半径为: .
.同理解得:
 .
.∴

∴△ADC是直角三角形,∠ADC=90°;
(3)设圆锥底面半径为r 则有
 ,解得:
,解得: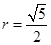 .所以圆锥底面半径为
.所以圆锥底面半径为 .
.
练习册系列答案
相关题目
 =2π,判断直线DC与⊙O的位置关系,并说明理由.
=2π,判断直线DC与⊙O的位置关系,并说明理由.



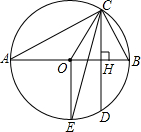
 的中点,连接0E,CE.求证:CE平分∠OCD.
的中点,连接0E,CE.求证:CE平分∠OCD.




