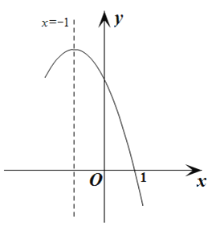ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНax2Љ4ax+3ЃЈaЁй0ЃЉгыХзЮяЯпyЃН![]() +kОљОЙ§ЕуAЃЈ1ЃЌ0ЃЉЃЎжБЯпxЃНmдкетСНЬѕХзЮяЯпЕФЖдГЦжсжЎМфЃЈВЛгыЖдГЦжсжиКЯЃЉЃЎКЏЪ§yЃНax2Љ4ax+3ЃЈxЁнmЃЉЕФЭМЯѓМЧЮЊG1ЃЌКЏЪ§yЃН
+kОљОЙ§ЕуAЃЈ1ЃЌ0ЃЉЃЎжБЯпxЃНmдкетСНЬѕХзЮяЯпЕФЖдГЦжсжЎМфЃЈВЛгыЖдГЦжсжиКЯЃЉЃЎКЏЪ§yЃНax2Љ4ax+3ЃЈxЁнmЃЉЕФЭМЯѓМЧЮЊG1ЃЌКЏЪ§yЃН![]() +kЃЈxЁмmЃЉЕФЭМЯѓМЧЮЊG2ЃЌЭМЯѓG1гыG2КЯЦ№РДЕУЕНЕФЭМаЮМЧЮЊGЃЎ
+kЃЈxЁмmЃЉЕФЭМЯѓМЧЮЊG2ЃЌЭМЯѓG1гыG2КЯЦ№РДЕУЕНЕФЭМаЮМЧЮЊGЃЎ
ЃЈ1ЃЉЧѓaЁЂkЕФжЕЃЎ
ЃЈ2ЃЉЕБmЃН![]() ЪБЃЌЧѓЭМаЮGЩЯyЫцxЕФдіДѓЖјМѕаЁЪБxЕФШЁжЕЗЖЮЇЃЎ
ЪБЃЌЧѓЭМаЮGЩЯyЫцxЕФдіДѓЖјМѕаЁЪБxЕФШЁжЕЗЖЮЇЃЎ
ЃЈ3ЃЉЕБЉ2ЁмxЁм![]() ЪБЃЌЭМаЮGЩЯзюИпЕуЕФзнзјБъЮЊ2ЃЌЧѓmЕФжЕЃЎ
ЪБЃЌЭМаЮGЩЯзюИпЕуЕФзнзјБъЮЊ2ЃЌЧѓmЕФжЕЃЎ
ЃЈ4ЃЉЕБжБЯпyЃН2mЉ1гыЭМаЮGга2ИіЙЋЙВЕуЪБЃЌжБНгаДГіmЕФШЁжЕЗЖЮЇЃЎ
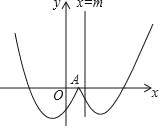
ЁОД№АИЁПЃЈ1ЃЉaЃН1ЃЌkЃНЉ2ЃЛЃЈ2ЃЉxЁмЉ1Лђ![]() ЁмxЁм2ЃЛЃЈ3ЃЉmЃН2Љ
ЁмxЁм2ЃЛЃЈ3ЃЉmЃН2Љ![]() Лђm=Љ1+2
Лђm=Љ1+2![]() ЃЛЃЈ4ЃЉЉ
ЃЛЃЈ4ЃЉЉ![]() ЃМmЁм1Љ
ЃМmЁм1Љ![]() ЃЌmЃН0ЃЌ3Љ
ЃЌmЃН0ЃЌ3Љ![]() ЁмmЃМ1+
ЁмmЃМ1+![]() ЃЛ
ЃЛ
ЁОНтЮіЁП
ЃЈ1ЃЉАбAЕузјБъДњШыСНИіКЏЪ§НтЮіЪНжаЃЌБуПЩЧѓЕУД§ЖЈЯЕЪ§aКЭkЃЛ
ЃЈ2ЃЉИљОнЧщПіЃЌЛГіКЏЪ§ЭМЯѓЃЌНсКЯКЏЪ§ЭМЯѓЧѓНтЃЛ
ЃЈ3ЃЉНЋmЗжСНжжЧщПіЛЭМЬжТлЃЛ
ЃЈ4ЃЉЕкЫФЮЪашвЊЛЭМевЕНЫФИіСйНчЕуЃЌНсКЯЭМЯѓНтЬтЃЎ
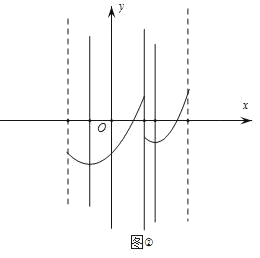
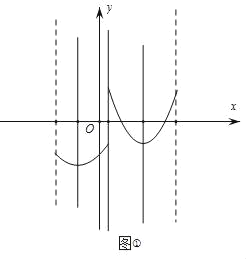
НтЃКЃЈ1ЃЉЁпХзЮяЯпyЃНax2Љ4ax+3ЃЈaЁй0ЃЉгыХзЮяЯпyЃН![]() +kЭМЯѓG1гыОљОЙ§ЕуAЃЈ1ЃЌ0ЃЉ
+kЭМЯѓG1гыОљОЙ§ЕуAЃЈ1ЃЌ0ЃЉ
ЁрaЉ4a+3ЃН0ЃЌ![]() ЁС22+kЃН0ЃЌ
ЁС22+kЃН0ЃЌ
НтЕУaЃН1ЃЌkЃНЉ2ЃЛ
ЃЈ2ЃЉЁпyЃНx2Љ4x+3ЃНЃЈxЉ2ЃЉ2Љ1ЃЌ
ЁрЭМЯѓG1гыЕФЖдГЦжсЮЊжБЯпxЃН2ЃЌ
ЁпyЃН![]() Љ2ЃЌЁрЭМЯѓG2гыЕФЖдГЦжсЮЊжБЯпxЃНЉ1ЃЌ
Љ2ЃЌЁрЭМЯѓG2гыЕФЖдГЦжсЮЊжБЯпxЃНЉ1ЃЌ
ЁрЕБmЃН![]() ЪБЃЌЭМаЮGЩЯyЫцxЕФдіДѓЖјМѕаЁЪБxЕФШЁжЕЗЖЮЇЪЧxЁмЉ1Лђ
ЪБЃЌЭМаЮGЩЯyЫцxЕФдіДѓЖјМѕаЁЪБxЕФШЁжЕЗЖЮЇЪЧxЁмЉ1Лђ![]() ЁмxЁм2ЃЛ
ЁмxЁм2ЃЛ
ЃЈ3ЃЉЕБЉ1ЃМmЃМ1ЪБЃЌm2Љ4m+3ЃН2 ЃЈШчЭМ1ЃЉ
НтЕУm1ЃН2Љ![]() ЃЌm2ЃН2+
ЃЌm2ЃН2+![]() ЃО1ЃЈЩсШЅЃЉ
ЃО1ЃЈЩсШЅЃЉ
ЕБ1ЃМmЃМ2ЪБЃЌ![]() ЃЈm+1ЃЉ2Љ2ЃН2 ЃЈШчЭМ2ЃЉ
ЃЈm+1ЃЉ2Љ2ЃН2 ЃЈШчЭМ2ЃЉ
НтЕУm1ЃНЉ1+2![]() ЃЌm2ЃНЉ1Љ2
ЃЌm2ЃНЉ1Љ2![]() ЃМ1ЃЈЩсШЅЃЉ
ЃМ1ЃЈЩсШЅЃЉ
ЃЈ4ЃЉЕБжБЯпyЃН2mЉ1гыyЃНЃЈxЉ2ЃЉ2Љ1ЃЌxЃНmЯрНЛЪБЃЌ
2mЉ1ЃНЃЈmЉ2ЃЉ2Љ1ЃЌ
ЁрmЃН3+![]() ЃЌmЃН3Љ
ЃЌmЃН3Љ![]() ЃЛ
ЃЛ
ЕБжБЯпyЃН2mЉ1гыyЃН![]() Љ2ЃЌxЃНmЯрНЛЪБЃЌ
Љ2ЃЌxЃНmЯрНЛЪБЃЌ
2mЉ1ЃН![]() Љ2
Љ2
ЁрmЃН1+![]() ЃЌmЃН1Љ
ЃЌmЃН1Љ![]() ЃЌ
ЃЌ
ЕБyЃН2mЉ1ЃНЉ2ЪБЃЌmЃНЉ![]() ЃЌ
ЃЌ
ЕБyЃН2mЉ1ЃНЉ1ЪБЃЌmЃН0ЃЌ
ЁрЉ![]() ЃМmЁм1Љ
ЃМmЁм1Љ![]() ЃЌmЃН0ЃЌ3Љ
ЃЌmЃН0ЃЌ3Љ![]() ЁмmЃМ1+
ЁмmЃМ1+![]() ЃЛ
ЃЛ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ