题目内容
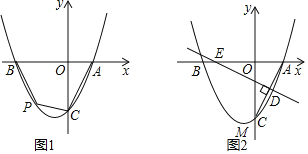
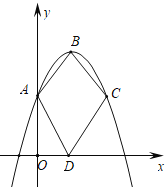
【题目】如图，在平面直角坐标系中，抛物线y＝﹣x2+3x+2与y轴交于点A，点B是抛物线的顶点，点C与点A是抛物线上关于对称轴对称的两个点，点D在x轴上运动，则四边形ABCD的两条对角线的长度之和的最小值为_____．
【答案】
【解析】
先将函数化为顶点式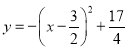
，所以顶点坐标
，对称轴为直线
，BD最小值为
，又点C与点A是抛物线上的两个对称点，对称轴为直线，所以C（3，2），AC＝3，因此四边形ABCD的两条对角线的长度之和AC+BD的最小值为
．
解：∵y＝﹣x2+3x+2＝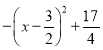
，
∴，对称轴为直线
∴当BD⊥x轴时，BD最小，BD＝
令x＝0，则y＝2，
∵C与点A是抛物线上关于对称轴对称的两个点，对称轴为直线，
∴C（3，2）
∴AC＝3，
四边形ABCD的两条对角线的长度之和AC+BD的最小值为
，
故答案为．
【题目】九年级孟老师数学小组经过市场调査，得到某种运动服的月销量y（件）是售价x（元/件）的一次函数，其售价、月销售量、月销售利润w（元）的三组对应值如表：
售价x（元/件） | 130 | 150 | 180 |
月销售量y（件） | 210 | 150 | 60 |
月销售利润w（元） | 10500 | 10500 | 6000 |
注：月销售利润＝月销售量×（售价﹣进价）
（1）求y关于x的函数解析式（不要求写出自变量的取值范围）；
（2）运动服的进价是 元/件；
（3）当售价是多少时，月销售利润最大？最大利润是多少元？
【题目】为引导学生广泛阅读文学名著，某校在七年级、八年级开展了读书知识竞赛，该校七、八年级各有学生
人，各随机抽取
名学生进行了抽样调查，获得了他们知识竞赛成绩(分)，并对数据进行整理、描述和分析．下面给出了部分信息．
七年级:
八年级:
成绩人数 |
|
|
|
|
|
七年级 |
|
|
|
|
|
八年级 |
|
|
|
|
|
平均数、中位数、众数如表所示:
年级 | 平均数 | 中位数 | 众数 |
七年级 |
|
|
|
八年级 |
|
|
|
根据以上信息，回答下列问题:
，
，
_
该校对读书知识竞赛成绩不少于
分的学生授予“阅读小能手”称号，请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有 人；
结合以数据，你认为哪个年级读书知识竞赛的总体成绩较好，说明理由
