题目内容
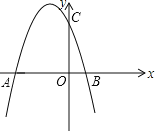
【题目】抛物线![]() 经过点(1,0),且对称轴为直线
经过点(1,0),且对称轴为直线![]() ,其部分图象如图所示.对于此抛物线有如下四个结论:①
,其部分图象如图所示.对于此抛物线有如下四个结论:①![]() <0; ②
<0; ②![]() ;③9a-3b+c=0;④若
;③9a-3b+c=0;④若![]() ,则
,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值.其中正确结论的序号是( )
时的函数值.其中正确结论的序号是( )
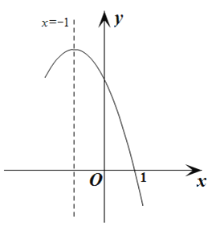
A.①③B.②④C.②③D.③④
【答案】D
【解析】
①根据抛物线开口方向、对称轴、与y轴的交点即可判断;
②根据抛物线的对称轴方程即可判断;
③根据抛物线y=ax2+bx+c经过点(1,0),且对称轴为直线x=﹣1可得抛物线与x轴的另一个交点坐标为(﹣3,0),即可判断;
④根据m>n>0,得出m﹣1和n﹣1的大小及其与﹣1的关系,利用二次函数的性质即可判断.
解:①观察图象可知:
a<0,b<0,c>0,∴abc>0,
所以①错误;
②∵对称轴为直线x=﹣1,
即﹣![]() =﹣1,解得b=2a,即2a﹣b=0,
=﹣1,解得b=2a,即2a﹣b=0,
所以②错误;
③∵抛物线y=ax2+bx+c经过点(1,0),且对称轴为直线x=﹣1,
∴抛物线与x轴的另一个交点为(﹣3,0),
当a=﹣3时,y=0,即9a﹣3b+c=0,
所以③正确;
∵m>n>0,
∴m﹣1>n﹣1>﹣1,
由x>﹣1时,y随x的增大而减小知x=m﹣1时的函数值小于x=n﹣1时的函数值,故④正确;
故选:D.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为引导学生广泛阅读文学名著,某校在七年级、八年级开展了读书知识竞赛,该校七、八年级各有学生![]() 人,各随机抽取
人,各随机抽取![]() 名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
七年级:
![]()
八年级:
![]()
成绩人数 |
|
|
|
|
|
七年级 |
|
|
|
|
|
八年级 |
|
|
|
|
|
平均数、中位数、众数如表所示:
年级 | 平均数 | 中位数 | 众数 |
七年级 |
|
|
|
八年级 |
|
|
|
根据以上信息,回答下列问题:
![]()
![]() ,
,![]() ,
,![]() _
_
![]() 该校对读书知识竞赛成绩不少于
该校对读书知识竞赛成绩不少于![]() 分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有 人;
分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有 人;
![]() 结合以数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由
结合以数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由