题目内容
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() 、
、![]() 、
、![]() .
.
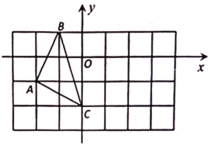
(1)点![]() 关于坐标原点
关于坐标原点![]() 对称的点的坐标为______;
对称的点的坐标为______;
(2)将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,画出旋转后得到的
,画出旋转后得到的![]() ;
;
(3)在(2)中,求边![]() 所扫过区域的面积是多少?(结果保留
所扫过区域的面积是多少?(结果保留![]() ).
).
(4)若![]() 、
、![]() 、
、![]() 三点的横坐标都加3,纵坐标不变,图形
三点的横坐标都加3,纵坐标不变,图形![]() 的位置发生怎样的变化?
的位置发生怎样的变化?
【答案】(1)(1,-1);(2)见详解;(3)![]() ;(4)图形
;(4)图形![]() 的位置是向右平移了3个单位.
的位置是向右平移了3个单位.
【解析】
(1)先求出点B的坐标,再点![]() 关于坐标原点
关于坐标原点![]() 对称的点的坐标即可;
对称的点的坐标即可;
(2)根据将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 的坐标特征即可得到A1、B1、C1的坐标,然后描点连线即可;
的坐标特征即可得到A1、B1、C1的坐标,然后描点连线即可;
(3) 利用扇形面积公式进行计算可得线段AC旋转时扫过的面积.
(4) ![]() 、
、![]() 、
、![]() 三点的横坐标都加3,即图形
三点的横坐标都加3,即图形![]() 的位置是向右平移了3个单位.
的位置是向右平移了3个单位.
解:
(1)∵点B的坐标是![]() ,
,
∴点![]() 关于坐标原点
关于坐标原点![]() 对称的点的坐标为(1,-1);
对称的点的坐标为(1,-1);
(2)如图所示,![]() 即为所求作的图形;
即为所求作的图形;
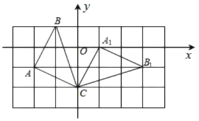
(3)∵![]() ,
,![]()
∴ ;
;
(4)∵![]() 、
、![]() 、
、![]() 三点的横坐标都加3,纵坐标不变,
三点的横坐标都加3,纵坐标不变,
∴图形![]() 的位置是向右平移了3个单位.
的位置是向右平移了3个单位.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
【题目】九年级孟老师数学小组经过市场调査,得到某种运动服的月销量y(件)是售价x(元/件)的一次函数,其售价、月销售量、月销售利润w(元)的三组对应值如表:
售价x(元/件) | 130 | 150 | 180 |
月销售量y(件) | 210 | 150 | 60 |
月销售利润w(元) | 10500 | 10500 | 6000 |
注:月销售利润=月销售量×(售价﹣进价)
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)运动服的进价是 元/件;
(3)当售价是多少时,月销售利润最大?最大利润是多少元?