题目内容
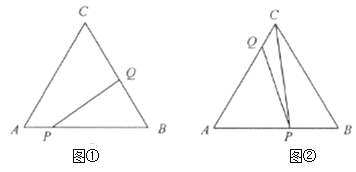
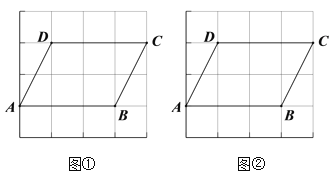
【题目】图①、图②均是4×4的正方形网格,每个小正方形的顶点称为格点,四边形ABCD的顶点均在格点上,仅用无刻度直尺,分别按下列要求画图.
(1)在图①中的线段CD上找到一点E,连结AE,使得AE将四边形ABCD的面积分成1:2两部分.
(2)在图②中的四边形ABCD外部作一条直线l,使得直线l上任意一点与点A、B构成三角形的面积是四边形ABCD面积的![]() .(保留作图痕迹)
.(保留作图痕迹)
【答案】(1)见解析. (2)见解析.
【解析】
(1)利用面积法,数形结合的思想,求出AE解决问题即可.
(2)如图②中,取格点M,N,K,连接MN,MK可得格点T,R,作直线TR,直线TR即为所求.
解:(1)如图,线段AE即为所求.
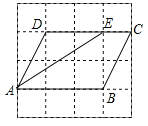
∵S四边形ABCD=3×2=6,S△ADE=![]() ×2×2=2.
×2×2=2.
∴![]() ;
;
(2)如图所示:直线TK为所求;
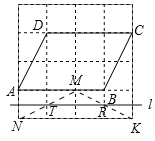
∵S四边形ABCD=3×2=6,
又∵![]() ,
,![]() ,
,
∴![]() ;
;
∴直线l∥AB,并且在AB的下方,距离AB等于![]() 个单位长度.
个单位长度.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
【题目】某校举行“汉字听写”比赛,每位学生听写汉字40个,比赛结束后随机抽查部分学生听写“正确的字数”,以下是根据抽查结果绘制的统计图表.
频数分布表
组别 | 正确的字数 | 人数 |
| 0.5~8.5 | 10 |
| 8.5~16.5 | 15 |
| 16.5~24.5 | 25 |
| 24.5~32.5 |
|
| 32.5~40.5 |
|
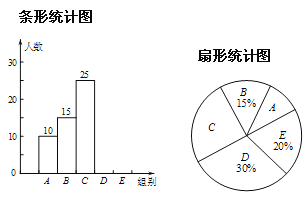
根据以上信息解决下列问题:
(1)补全条形统计图;
(2)扇形统计图中“![]() 组”所对应的圆心角的度数是_________;
组”所对应的圆心角的度数是_________;
(3)若该校共有1210名学生,如果听写正确的字数少于25,则定为不合格;请你估计这所学校本次比赛听写不合格的学生人数.