题目内容
把(x2﹣x+1)6展开后得a12x12+a11x11+…a2x2+a1x1+a0,则a12+a10+a8+a6+a4+a2+a0= .
365
试题分析:由题意可列出式子:(x2﹣x+1)6=a12x12+a11x11+…+a2x2+a1x1+a0,再将x=1及x=﹣1代入式子,即可得出两个多项式,再将两多项式相加即可求解.
解:∵(x2﹣x+1)6=a12x12+a11x11+…+a2x2+a1x1+a0,
∴当x=1时,(x2﹣x+1)6=a12+a11+…+a2+a1+a0=1,①;
当x=﹣1时,(x2﹣x+1)6=a12﹣a11+…+a2﹣a1+a0=36=729,②
∴①+②=2(a12+a10+a8+a6+a4+a2+a0)=730,
∴a12+a10+a8+a6+a4+a2+a0=365.
故此题答案为:365.
点评:本题考查了多项式乘多项式,主要是要找对x=1及x=﹣1这两个特殊的值.

练习册系列答案
相关题目
 .
.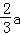 ,则该长方体的体积为 _________ .
,则该长方体的体积为 _________ .